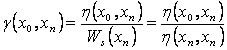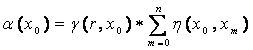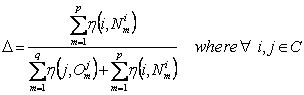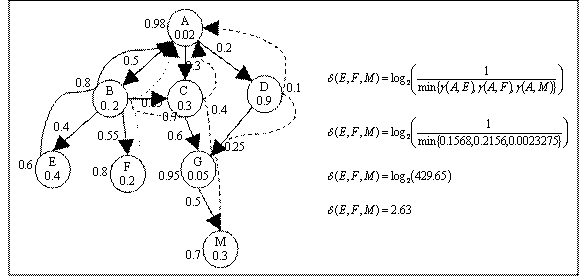Acknowledgements
I am most grateful to my advisor Dr. Javed I
Khan for his encouragement and vision. Dr. Khan has the ability to make others
envision ideas and inspire creativity. I
would like to thank Dr. Khan for getting me interested in research and helping
me at every stage.
I am also thankful for the members of the
MediaNet Lab, Nouman, Asrar, and Oleg for their support and advice. I would like
to thank my project mates Yongbin Ma and Sujatha Gnyaneshwaran who helped me in
my research and for contributing to my thesis, without which this effort
wouldn’t have been possible. I would like to thank my close friends and
roomates, Sajid, Siddharth, Kailas,
Amit, Srinivas, Shandy, Saby and Pradeep for their constant support.
I would like to thank my family whom I
dearly miss and without whose blessings none of this would have been possible.
I thank my mom and dad for always believing in me and standing by me through
everything. Particularly I thank my grand mom and grand dad, my love and
respect for whom, is beyond measure.
Abstract
Semantic analysis of educational resources
is a very interesting problem with numerous applications. Like any design
process, educational resources also have basic elements of design and
reproduction. In the process of designing test problems, these elements are in the
form of information objects. Course knowledge can be represented in the form of
prerequisite relation based ontology using which, assessment and information
extraction from test problems is possible. We propose a language schema based
on Web Ontology Language (OWL) for formally describing course ontologies. Using
this schema, course ontologies can be represented in a standard and sharable
way. An evaluation system acts as the backend for the design and re-engineering
system. This research aims at automating the process of intelligent evaluation
of test-ware resources by providing qualitative assessment of test problems.
Some synthetic parameters for the assessment of a test problem in its concept
space are introduced. The parameters are tested in some real world scenarios
and intuitive inferences are deduced predicting the performance of the
parameters. It is observed that the difficulty of a question is often a
function of the knowledge content and complexity of the concepts it tests.
Introduction and
Background
Since the advent of the Web a great
optimism has been created about online sharing of course material. Many educators
worldwide today maintain course websites with online accessible teaching
materials. The primary use of these web-sites is for dispensing lecture
materials to immediate students. There have been many organized attempts as well
to create large digital courseware libraries to promote sharing. Some of the
significant efforts in this direction are NIST Materials Digital Library
Pathway [2, 3], NSDL Digital Libraries in science, technology, engineering and
mathematics (STEM) [10], OhioLink [4], ACM Professional Development Centre with
over 1000 computer science courses [5], etc. Most universities, colleges and
even schools now actively encourage online course material dispensing through
portals. MIT’s Open Course Ware (OCW)
project [7] has more than 1000 course materials freely available, Universia [6]
maintains translated versions of OCW courses in 11 languages, China Open
Resources for Education (CORE) has a goal to
include Chinese versions of the OCW for over 5000 courses, NSDL has focused on
collecting specialized learning materials and currently has more than 1000 such
collections [8], Centre for Open and Sustainable Learning [9] at the Utah State
University, etc. the amount of digital courseware content available online is huge.
Surprisingly, the real sharing of the materials among the educators is still
very low. In OCW it has been noted that only 16% of the users are educators out
of which not more than 26% use it for planning their course or teach a class [10].
The actual reuse for most sites is mostly unreported and possibly lower.
Surprisingly despite such massive intention, organized efforts and the market,
effective sharing of courseware among teachers is almost non existent. A fresh
and critical look has to be undertaken to tackle the central problem of sharing
learning objects. It seems good courseware is the product of complex design [12,
13]. The process of teaching requires continuous innovation, adaptation and
creative design on the part of the teacher. Unfortunately the current form and
status of courseware doesn’t aid to this process at all. Teaching is a high
level cognitive activity of knowledge organization and dissemination and
requires complex and continuous customization.
Most courseware today, on the web or
otherwise, is not accompanied with a conceptual design. Any composition, engineering
design or courseware or an art work always takes place in the context of a
conceptual design space. The conceptual context is the most important factor in
any formative learning process. Consider a lecturer giving a presentation on
some topic. If the lecturer simply talks about the presentation topic without
giving any reference to a slide or a diagram, it is very difficult to
understand. Conversely if the lecturer just presents the slides without
explaining them in some context, the presentation remains incomplete. There is
no well formed encoding principle for capturing and sharing this invisible
design without which the course materials significantly loose much of their reusability.
In desperate cases, teacher has to manually reverse engineer the design from
the courseware. Therefore, it is not surprising that instructors and educators
find it easier to build the course materials from scratch rather than reusing
online available resources. The background design of the course material is
vital for creation and reengineering of courseware. It is very unlikely that
without the design, finished courseware available will ever be used creatively.
Currently the web is huge repository
of assorted digital resources without much reusability. Most educational
content is scattered, replicated and not linked to each other by any kind of
relationship. To make this digital content reusable, sharing the metadata
associated with it is necessary. A clear distinction has to be made between
knowledge and information. Knowledge is the means by which intelligent design
and sharing of test-ware and other web resources is possible. The main problem
of information on the web is that it is hardly machine usable [11]. To make the
data on the web reusable it is necessary to have information about the data
itself. Thus the Meta information associated with the
actual data is just as important as the data. Palazzo et.al. [13] address this
problem and propose a system for courseware authoring taking into account the
student learning style, technical background, presentation preferences and
other inclinations.
Traditionally
concepts maps are used to represent the backend context for the course
knowledge. Many efforts [16, 17, 18, 19] have gone into representing course
knowledge using concept maps. In the recent past ontologies progressively are being
used to represent structured information in a hierarchical format. Concept maps
offer a means to represent hierarchical knowledge; however they are too
expressive and consequently contain more information and semantic relationships
than necessary for effective computation. Ontologies provide a means to
effectively map this knowledge into concept hierarchies. Course ontology,
particularly, can be roughly defined as a hierarchical representation of the
topics involved in the course, connected by relationships with specific
semantic significance. Using ontologies for course concept hierarchies in the
domain of education is only obvious. Currently the process of designing of test
problems is completely manual, based on human experience and cognition. Design
of test problems also follows the basic principles of any engineering design
process. The primary elements of design in this case are the information
objects. Much effort has been put in the creation and reusability of these
information objects called as the learning objects. The Learning Object
Metadata (LOM) [26] standard for the representation of information about
educational resources is the product of this effort. Recent standardization of
semantic representation standards like RDF and OWL offers great technical
platform to represent the concept knowledge space symbolized by ontologies. The
representation of meta data for educational resources greatly improves it
machine usability. These progressive steps taken in the field of knowledge and
metadata representation now provide a great platform for researchers and
theorists to create resourceful and innovative applications which effectively
utilize the background knowledge in a particular domain to intelligently and
automatically design, compose, evaluate, reengineer and share information rich
resources like courseware, web resources, educational materials etc.
1.1.
Related Work
There have been numerous attempts to
quantify the complexity of problems [14, 15, 16, 17, 21]. The approaches to
problem difficulty assessment can be distinguished into two types, knowledge
based approaches and cognition based approaches. Researchers which follow
knowledge based approach generally present mathematical models for calculating
difficulty of a problem based on the knowledge it tests. The cognitive
researchers look at the problem from learning point of view and try to find
answers from the student and education perspective.
Li and Sambasivam [17] experiment
with static knowledge structure of computer architecture course to compute
problem difficult. The difficulty is calculated based on normalized weights of
the concepts connected to and from the question. Kou, et.al. [14, 15] propose a
very innovative technique to represent concept maps using information objects.
These objects act as input to a system which calculates difficulty. Difficulty
is considered a function of numerous factors like, number of attributes,
learning sequence of concepts, concept depth, number of unknown parameters, and
number of given attributes mathematical complexity etc. However the system does
not calculate difficulty for complex problems, i.e. problems based on more that
one concept. Palazzo, et. al. [12] provide a great representation for course
knowledge. Though they do not consider the problem of difficulty assessment,
they provide an excellent means for course ware authoring based on course
ontologies linked with prerequisite relationships. The main problem with these
approaches is that no solid course representation technique is used
consistently. The representations used are often rigid, incomplete and
incomputable. Li and Sambasivam’s static knowledge structures are intuitively
generated structures where weights are allocated on parent child relationship
without any external considerations. Kou et.al. use a number of other factors
the values for which are calculated mostly empirically and are highly
subjective.
The other group is the one of
cognitive and educational researchers. Lee, F-K and Heyworth R., attempt to calculate the difficulty of a
problem based on factors like, perceived number of difficult steps, steps
required to finish the problem, number of operations in the problems expression
and students degree of familiarity with the question. Studies by Croteau, Heffernan & Koedinger
(2004), Koedinger & Nathan, (1999), [24, 25, 26, 27] try to figure “why
algebra word problems are difficult?” They propose difficulty measures which
are based on arithmetic and symbolization in a problem. The reasoning behind
this is that, greater the number of symbols in an arithmetic problem, greater
is the difficulty. Cognitive research also reason that much of the difficulty
children experience with word problems can be attributed to difficulty in
comprehending abstract or ambiguous language [44].
This thesis follows a purely
knowledge based approach to assessment of problem difficulty. The main problem
with previous works is that they fail to give a coherent representation of the
knowledge domain. We present a novel approach to course ontology representation
which is standard and coherent, and propose some assessment parameters for
problem complexity computation.
1.2.
Thesis contribution
In this thesis we present a novel
approach to course knowledge representation using course ontologies, in an
expressible and computable format using has-prerequisite
relationships where concepts involved in teaching a course are arranged in
hierarchical order of their importance. It differs from traditional ontologies
most significantly in that, it is not IS-A relation based and it is not a
directed acyclic graph (DAG) as most traditional ontologies. A schema language
is developed called, Course Ontology Description Language (CODL) for
representing course ontologies which can provide a framework for encoding and
sharing courseware. It is based on OWL and provides a powerful framework for
representing course ontologies in a standard and sharable way. Another original
approach for specifically pointing out areas in ontologies of maximum relevance
is given. This approach allows for the effective processing of only the
relevant part of the ontology by which the computation time and resources are
effectively saved.
This thesis investigates the
properties of test problems by following a purely knowledge based approach for
assessment using course ontologies. Here assessment refers to evaluation of
test problems for their knowledge content and complexity. We isolate the main
pedagogical challenge as finding measurable quantities that can provide
guidance in the process of automatic evaluation. We reason that the qualitative
assessment of problems in their concept space is a very important step in
making online testing, e-learning or web based pedagogy even remotely
effective. Standardizing problems by evaluating the complexity can be a backend
system with immense potential for test-ware composition and sharing
applications. It has the potential to make the already available test-ware
resources on the web reusable. These evaluation parameters are calculated by
applying mathematical formulations to the course ontology. The parameter
performance is also tested in real world test scenarios and it is shown that
they are very good indicators of problem complexity. Interesting logical
inferences are made from the observed behavior of evaluation parameters with
respect to the knowledge a problem tests and the observed performance of the
students. The semantic evaluation system can intuitively be applied in varied
application areas like automatic test and question generation and solution
grading. We present a few possible applications of this system.
Course knowledge representation using ontologies
Automated design and evaluation involve
formal mathematical assessment models unlike cognition based models in humans.
These cognition based assessment models for design and evaluation are developed
by the human mind over a period of time, by learning and collecting and
assessing information from corpora of incoming knowledge. Recently great deal
of research is being done to make these corpora of knowledge available for
machines. A machine understandable and computable assessment system therefore
is essential. This body of knowledge is represented using techniques from
knowledge representation like semantic networks and ontologies. Ontology is a
method for representing elements in a domain or corpus of knowledge in a
hierarchical fashion and links these elements with semantic relationships.
The corpus of course knowledge is
hypothetically divided into two tiered description framework namely, concept
space and resource space. The course ontology is the conceptual representation
of the concept space graph, where in concepts are linked to each other using
semantic relations. The resource space gives the description of actual
resources for the corresponding concepts from the concept space. The course
concept
space,
symbolized by course ontology, is built using a language variant of Web
Ontology Language, OWL [31]. The language is designed to harness maximum
computability at the cost of reduced expressive power. The types of relations
and properties are kept at minimum. The second tier of description, the
resource space, requires more expressiveness. LOM [28] developed for learning
object classification is used to provide the base elementary description for
the learning objects, the resources. In this section we discuss in detail the
definition, specification, and constructs for the language used to represent
course ontologies.
2.1.
Knowledge Representation Issues
In computer science and artificial intelligence,
knowledge representation is a technique by which knowledge about a particular
domain is structured to increase its usability. Knowledge representation
techniques are used in AI, cognitive science, and other fields for problem
solving, logical reasoning, data mining, question-answering, theorem proving,
neural networks, expert systems etc. Davis, Shrobe and Szolovits define
knowledge representation as a “set of ontological commitments” and “a medium of
pragmatically efficient computation” [45]. It means that knowledge
representation is set of vocabulary agreed upon, to represent knowledge which
is practical and computable at the same time. It is important for the knowledge
representation to be expressible and computable. This in turn brings us to the
problem of granularity of information in course ontology. The granularity of
the ontology is an important factor to consider while building the course
ontology. The ontology can range from being fine-grained to coarse-grained. A finer
grained ontology will contain more concepts in detail and more implicit
relationships between unrepresented concepts can be discovered. Finer the
ontology, the application will have more knowledge to work with giving better results.
But defining a finely grained expressive ontology is costly in terms of
computation. As more and more concepts and relationships are defined and represented,
more is the information to be processed. At the same time, though coarse
grained ontologies are computable, they do not have enough information needed
for better results. The depth of the knowledge to be represented is therefore
an important question in representing any kind of knowledge. Most available
finished materials today are coarse granular. Unfortunately, this is not
suitable for semantic evaluation. Any design system requires the basic ability
to transcend between multiple levels of granularity. In other words the
mechanism of decomposing as well as re-composition is fundamental.
2.2.
Course Ontology
Ontologies derive their roots from
philosophy. In philosophy ontologies are used to represent the account of what
exists. In computer science they are generally defined as “a specification of a
conceptualization” [46]. Ontology is a data model that represents a domain and
is used to reason about the objects in the domain and the relations between
them. In the context of this research the domain is that of a “course”, the objects are “concepts in the course” and the
relations between the concepts are that of “has-prerequisite”.
Simply put, ontology is a group of concepts organized to reflect the
relationships between the concepts. It is a method of specification and
speculation about information. In recent past ontologies are increasingly being
used to represent information in various domains like biological sciences,
accounting and banking, intelligence and military information, geographical
systems, language based corpus, cognitive sciences, common sense systems etc. The
applicability of computer science is in the efficient representation of these
ontologies and the subsequent algorithmic processing. Most ontologies today are
so extensive in the breadth of knowledge that processing of these ontologies
becomes almost impossible and a gargantuan computation task. There needs to be
a way to efficiently process the relevant information in these ontologies to
give optimum results in minimum time and complexity of computation. We present
a method which points out to a portion of the ontology which is of maximum
relevance and then start processing on this portion. The size of this portion
of the ontology, which we call as the projection graph, can be changed
according to the desired semantic significance.
Ontologies are made up of
individuals, classes, attributes and relationships. Individuals, the
instantiations of classes, form the basic elements of ontology. Classes are
abstract concepts which define and may contain other classes or individuals or
both. Attributes are the properties of individuals or relationships. The name
of the property is the attribute under consideration while the values of
attributes can take form in various data types ranging from integers, strings,
boolean etc. An individual is also allowed to have multiple attributes in the
definition. Relationships are the way the concepts in the ontology are
structured with respect to each other. Relations can be thought of as
attributes whose value is another object in the ontology and is used to define
the relationship between two or more different objects. Semantic relations particularly
important in the context of ontologies are: Meronymy (part-of), Holonymy, Hypernymy,
and Hyponymy. The has-prerequisite relationship is like holonymy relationship,
where in the child node is a part of the parent node. However, in the context
of course ontology, the part-of
semantics refers to the prerequisite understanding of the child node needed to
understand the parent node. On the whole the course ontology is constructed in
such a hierarchical fashion that the children of node represent the knowledge required
to understand the parent node, and their children represent the knowledge
required to
understand them,
so on and so forth. The ontology is created using the principle of
“constructivism” borrowed from learning theory. The theory states that any new
learning occurs in the context of and on the basis of already acquired
knowledge. We use this theory to practically implement the has-prerequisite
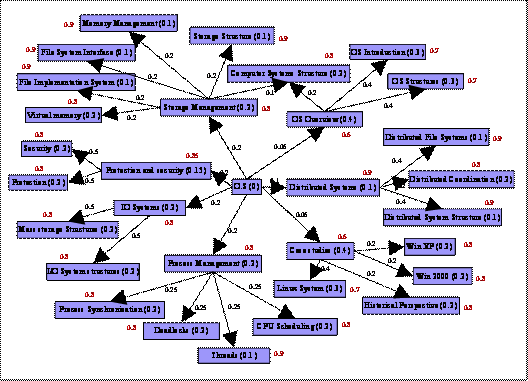
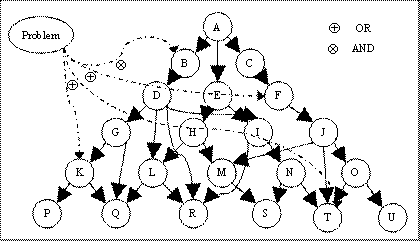
relationship based course ontology. See in Figure 2.2. “Process Management” is
the prerequisite of “OS”.
A node is characterized by two
values namely, self-weight and pre-requisite weight. The self-weight of a
concept node is the value or the knowledge which is inherent to that node
itself. It means that, the self-weight is the numerical realization of the
knowledge required to grasp the concept, not in its entirety, but in partiality
with respect to itself. To understand the concept entirely, knowledge of the
prerequisite concepts is also required, which is given by the prerequisite
weight of the node. It gives the numerical realization of the importance of the
understanding of the prerequisite concepts in the absolute understanding of a
parent concept. Another value which characterizes the course ontology
representation is the link weight. The link weight again is the numerical
realization of the semantic importance of child concept to the parent concept.
Child concepts imperative in the understanding of parent concepts will have a
greater link weights than the others. Thus the course ontology representation is
a collection of concepts nodes with self-weights and prerequisite weights and
has-prerequisite relationships linking these nodes with a value attribute given
by the link weight.
2.3.
Representation Standards
The recent advances in Semantic Web
representation languages such as RDF, RDF schema [35], and recently OWL [29,
30] now provide a promising
technology basis for metadata representation. The course ontology is
represented using OWL. OWL offers a convenient platform for the representation
of hierarchical concepts like that in the course ontology. There are 3 sub
categories of the OWL language namely, OWL Lite, OWL DL and OWL Full. Among
these profiles OWL Full offers maximum expressiveness but it does not guarantee
computability. OWL Lite offers computability by restricting expression power of
the language. OWL DL (OWL Description Logic) offers a balance between the
expressiveness of OWL Full and the computability of OWL Lite. It has all the
language constructs from OWL Full, but can only be used with restrictions. The
differences between the three categories are explained below.
- OWL Full: It contains all the OWL language constructs
and provides free unconstrained use of RDF constructs. In OWL Full the
construct owl:Class is
equivalent to rdfs:Class, unlike in OWL Lite and OWL DL where owl:Class
is a proper sub class of rdfs:Class.
Most importantly, in OWL Full, individuals can be treated as classes. It
means that, individual of class TypeOfCarSedan, HondaAccord,
can also be a class, containing all Honda accord cars. In OWL Full data
values can also be considered as individual. Thus ObjectProperty
and DatatypeProperty
are not disjoint and in fact the latter is the sub class of the former. A rdfs:Resource
is equivalent to owl:Thing
in OWL Full, which means that any Thing can be a
resource. OWL Full provides the expressivity of OWL with flexibility and
meta modeling feature of RDF.
- OWL DL: It has the same constructs as in OWL Full but
governed by some additional restrictions. In OWL DL an individual cannot
be treated as a class, which means that all classes, data types, data type
properties, object properties, annotation properties, ontology properties,
individuals, data values etc. are all disjoint. This means that data type
properties in OWL DL can never be inverse, inverse functional, symmetric
and transitive. Also no cardinality can be placed on transitive
properties, to maintain decidability of reasoning [31]. Most RDFS
vocabulary cannot be used in OWL DL. Axioms must be well formed and always
refer to class names. In particular, the OWL DL restrictions allow the
maximal subset of OWL Full against which current research can assure that
a decidable reasoning procedure can exist for an OWL reasoner [30].
- OWL Lite: OWL Lite abides by all the restrictions OWL
DL puts on the use of the OWL language constructs. In addition, OWL Lite
forbids the use of owl:oneOf,
owl:unionOf, owl:complementOf, owl:hasValue, owl:disjointWith,
owl:DataRange. The subjects of all axioms in OWL Lite must
be identifiers or restrictions. The idea behind the OWL Lite expressivity
limitations is that they provide a minimal useful subset of language
features that are relatively straightforward for tool developers to
support. The language constructs of OWL Lite provide the basics for
subclass hierarchy construction: subclasses and property restrictions. In
addition, OWL Lite allows properties to be made optional or required. The
limitations on OWL Lite place it in a lower complexity class than OWL DL.
This can have a positive impact on the efficiency of complete reasoner for
OWL Lite. Implementations that support only the OWL Lite vocabulary, but
otherwise relax the restrictions of OWL DL, cannot make certain
computational claims with respect to consistency and complexity.
2.3.1 Course Ontology Description Language (CODL)
It is the language we define to
represent course ontologies. The schema for the course ontology description is mostly
adherent to OWL Lite, with a few extensions. OWL Lite is used because it
supports basic classification hierarchy and simple constraint features and due
to its computational advantages over the other sub languages. However,
representing the schema for our course ontology in OWL is an extremely non
trivial issue as we will see in the explanation for the schema. The CODL schema
is shown in the Figure 2.3. The elements of CODL defined course ontology are
header information, class definitions, property definitions and individuals.
1. owl:Ontology:
It is a collection of assertions
about the course ontology. This section can contain comments, version
information and imports for inclusion of other ontologies. For example, the
course ontology for a specific course, say “Operating Systems”, can include
another separate ontology for a course on “Calculus” from Mathematics. The CODL
schema provides a method for conformant exchange of course ontologies.
Ontological information about individuals appearing in multiple documents can
be linked in a principled way.
<owl:Ontology
rdf:about="###">
<rdfs:comment>A schema for CODL
(Course Ontology Description
Language)</rdfs:comment>
<rdfs:label>Course
Ontology</rdfs:label>
</owl:Ontology>
The owl:priorVersion element can be used to
reference the previous version of the ontology. Versioning can effectively be
done to different levels of granularity of the ontology. The owl:import
element, which takes rdf:resource element as its subject, is used to import
another ontology in to one ontology.
2. class:Concept:
The course ontology is structured in
the form of individual concepts arranged in a hierarchy. All the individuals in
the OWL representation are the instantiations of the class Concept. The class Concept is the super class which defines all
concepts in the course ontology, including the restrictions on the values of
the properties they can take. The class Concept has the rdfs construct of rdfs:subClassOf.
The sub class axiom is used to define the necessary conditions for belonging to
a sub class or a property restriction. OWL Lite requires the subject of the rdfs:subClassOf
statement to be a class identifier. The instances of the class Concept are
also instance of the universal class owl:Class in OWL, which comprises of all the classes
which can be legally defined in the vocabulary of OWL language. The object of
the sub class axiom is a property restriction. It describes an anonymous class,
namely a class of all individuals which satisfy the restriction.
<owl:Class
rdf:ID="Concept">
<rdf:comment>Course
ontology concept</rdfs:comment>
<rdfs:subClassOf
rdf:resource="http://www.w3.org/2002/07/owl#Class"/>
<rdfs:subClassOf>
<owl:Restriction>
<owl:onProperty
rdf:resource="#hasPrerequisite"/>
<owl:allValuesFrom
rdf:resource="Relation"/>
</owl:Restriction>
</rdfs:subClassOf>
</owl:Class>
For example, in the above property
restriction, the statement owl:Restriction
defines an anonymous class, all of whose instances satisfy the restriction on
properties hasPrerequisiteWeight.
The property restriction states that, for all instances of class Concept,
if they have a prerequisite (hasPrerequisite)
then it must belong to extension of Relation.
The extension of Concept
means the set of all the members of the class Concept.
3. class:Relation:
The class Relation is used to give values to the hasLinkWeight
property. In our representation, two instances of class Concept are connected by the property hasPrerequisite
which has a link weight value. Accordingly, we want to be able to link an
individual to another individual with a value and semantic relationship. These
kinds of relationships are called as n-ary
relationships [33]. There are two types of properties in the OWL world, object
properties which connect instances of classes to each other, and data type
properties which connect instance to data values. OWL does not offer means to
link individuals with data values. Therefore we make a very important abstraction
in the schema to form a separate class for Relations. The main objective of the class Relation
is to link two individuals of the class Concept with a data value. We first link
instance of the class Concept
to an instance of Relation,
and then link that instance again to instance of Concept.
<owl:Class rdf:ID="Relation>
<rdfs:subClassOf>
<owl:Restriction>
<owl:onProperty
rdf:resource="#connectsTo">
<owl:allValuesFrom
rdf:resource="#Concept">
</owl:Restriction>
</rdfs:subClassOf>
</owl:Class>
Thus by defining relationships
between individuals as another class, n-ary
relations can be defined in the schema and property restrictions can be
applied.
4. ObjectProperty:
hasPrerequisite
In our representation, hasPrerequisite
property links an instance of Concept
and instance of Relation.
The semantic relationship of hasPrerequisite
between two individuals is defined as an ObjectProperty.
<owl:ObjectProperty
rdf:ID="hasPrerequisite">
<rdfs:domain
rdf:resource="#Concept"/>
<rdfs:range
rdf:resource="#Relation"/>
</owl:ObjectProperty>
The rdfs:domain is a property feature which is
used to limit the domain of the individuals in which the property applies. If a
property relates an individual to another individual, and the property has a class
as one of the domains, then the individual must belong to that class. Here the
property is applicable in the domain of class Concept. It is possible to have more that one
domain. The rdfs:range
feature limits the individual the property may have as its value. This means
that if a property has range as a class, the instance of only that class can
have the property. In other words, if a property relates one individual to
another, and the property has class as its range, then the other individual
must belong to range class. When an instance of the concept class has the
property of hasPrerequisite,
the other individual to whom it relates to, must be from class Relation.
Domain and range both are global restrictions.
5. ObjectProperty:connectsTo
<owl:ObjectProperty
rdf:ID="connectsTo>
<rdfs:range
rdf:resource="Concept">
</owl:ObjectProperty>
This property is used to link
instance of Relation
to instance of Concept.
The property restriction on connectTo,
implies that all members of class Relation
which connectsTo
another member, the other member must be an individual of class Concept.
6. DatatypeProperty:
hasLinkWeight
A data type property links
individual to data values. Link weight is a characteristic of a relation therefore
hasLinkWeight
applies to instances of class Relation.
The range of the property is set by the resource xsd:float. For the purpose of computational ease
we set the values for all the concept and link properties between 0 and 1. In
OWL Lite the range of a property must be a class identifier. ObjectProperty
and DatatypeProperty
are not disjoint in OWL Full unlike in OWL Lite and DL and are both sub classes
of the rdf:Property
class. The hasLinkWeight
property links an instance of class Relation
to a data value.
<owl:DatatypeProperty
rdf:ID="hasLinkWeight">
<rdfs:domain
rdf:resource="#Relation"/>
<rdfs:range
rdf:resource="xsd:float"/>
</owl:ObjectProperty>
7. DatatypeProperty:
hasSelfWeight
hasSelfWeight
is used to define the self weight of a node. It too is applicable in the domain
of the class Concept
and range of values can be between 0 and 1.
<owl:DatatypeProperty
rdf:ID="hasSelfWeight">
<rdfs:domain
rdf:resource="#Concept"/>
<rdfs:range rdf:resource="xsd:float"/>
</owl:DatatypeProperty>
8. DatatypeProperty:
hasPrerequisiteWeight
This property is used to relate an
individual of the class Concept
to its prerequisite weight values. By definition, the summation of self weight
and prerequisite weight for a node is 1. Therefore this property is actually
redundant as the prerequisite weight values doesn’t need to be explicitly
specified and can be calculated from the self weight values. However this
property is included in the definition language, to incorporate the structural
changes needed in an ever growing ontology. Nodes can be added and subtracted
from the ontology, which may affect the prerequisite weight. Therefore this
property is included to explicitly specify the values in such cases.
<owl:DatatypeProperty
rdf:ID="hasPrerequisiteWeight">
<rdfs:domain rdf:resource="#Concept"/>
<rdfs:range rdf:resource="xsd:float"/>
</owl:DatatypeProperty>
9. Individuals:
<Concept
rdf:ID="MemoryManagement"/>
<Concept
rdf:ID="OS">
<hasPrerequisite>
<Relation
rdf:ID="relation_1">
<connectsTo
rdf:resource="#MemoryManagement"/>
<hasLinkWeight
rdf:resource="#0.2"/>
</Relation>
</hasPrerequisite>
<hasSelfWeight
rdf:resource="0.39"/>
<hasPrerequisiteWeight
rdf:resource="0.61"/>
</Concept>
This is an instance of a typical
individual in course ontology. Here the concept instance “MemoryManagement” is
a prerequisite for “OS”. Individuals are generally described by facts about
their class membership and their property values. Individual member “OS” is a
member of class Concept and has the property values for hasLinkWeight
as 0.2, hasSelfWeight
as 0.39 and hasPrerequisiteWeight
as 0.61.
The most important part of the
course ontology structure is the semantics between parent and child concepts.
The representation should be able to not only define prerequisite relationship
between them, but also define the value strength of this relationship. OWL does
not have provision to relate two individuals using data values. In CODL, we
define these kinds of n-ary relationships
by defining a separate class of relations. Therefore the tool which uses CODL
defined course ontology should be able to infer that, since connectsTo
links relation_1
and MemoryManagement and hasPrerequisite
links OS to relation_1,
MemoryManagement is prerequisite of OS.
Characteristics
of hasPrerequisite
and connecsTo
properties are as follows:
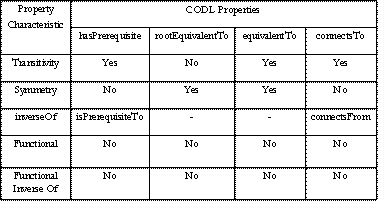
1. Transitivity:
hasPrerequisite(a,r),
hasPrerequisite(r,c) iff hasPrerequisite(a,c)
connectsTo(a,b),
connectsTo(b,c) iff connectsTo(a,c)
Both hasPrerequisite
and connectsTo
are transitive.
2. Symmetric:
hasPrerequisite
(a, b) ≠ hasPrerequisite (b, a)
connectsTo
(a, b) ≠ connectsTo (b, a)
Both hasPrerequisite
and connectsTo
are not symmetric.
3. Functional
Property:
hasPrerequisite
(a, b) and hasPrerequisite(a, c) does not imply b=c
connectsTo(a,
b) and connectsTo(a, c) does not imply b=c.
Both hasPrerequisite
and connectsTo
are not functional.
4. Inverse of: The
inverse properties of hasPrerequisite
and connectsTo
are isPrerequisiteTo
and connectsFrom
repectively.
hasPrerequisite(a,
b) iff isPrerequisiteTo(b, a) and;
connectsTo(a,
b) iff connectsFrom(b, a)
5. Inverse
Functional:
hasPrerequisite
(b, a) and hasPrerequisite(c, a) does not imply b=c
connectsTo(b,
a) and connectsTo(c, a) does not imply b=c.
Both hasPrerequisite
and connectsTo
are not inverse functional.
2.3.2 Extensions to CODL
In this section we define some more
properties to make extensions which can be incorporated in to the CODL schema
for making some powerful inferences from the language.
1. ObjectProperty:rootEquivalentTo
<owl:ObjectProperty
rdf:ID="rootEquivalentTo">
<rdf:range
rdf:resource="#Concept"/>
</owl:ObjectProperty>
The namespace declarations in OWL
ontology provide a means to reference names defined in other OWL ontologies.
The owl:import
element can be used to import the entire set of assertions made by the imported
ontology into the current ontology. However no current definition of import
allows us to specify a node as an entirely different ontology. The rootEquivalentTo
property provides a mechanism to expand a node in course ontology to a
completely new ontology. That means that, a node in course ontology is allowed
to be a root node of any other ontology.
<Concept
rdf:ID="OS">
<rootEquivalentTo
rdf:resource="#OperatingSystem"/>
...
</Concept>
This means that “OS”, which is an
instance of the class Concept,
and is rootEquivalentTo
the individual “OperatingSystem”, which is a member of the class Concept
specified by the range. The equivalence property for individuals’ owl:sameAs
can be used to the same effect. However, defining the property as restriction
on relations rather than concepts, allows for more freedom of expression in the
schema.
2. ObjectProperty:equivalentTo
<owl:ObjectProperty
rdf:ID="equivalentTo">
<rdf:range
rdf:resource="#Concept"/>
</owl:ObjectProperty>
This property provides a mechanism
to equate all the nodes within ontology, so that ultimately the whole ontology
is one node. It is important to note that relating all nodes by equivalentTo
property doesn’t actually mean that they are semantically equal. The purpose of
equivalentTo
property is only to unify the whole ontology as just an instance of the class Concept.
This has very powerful implications for importing and sharing ontologies with
different schemas. More power can be attributed to the representation by
interspersing different kinds of relationships within ontology. Thus the
ontology need not be based solely on hasPrerequisite relationship, but can also
have other relationships like those stated above.
2.4.
Mathematical representation of Concept Space
Graph (CSG)
The course ontology is
mathematically defined in the form of a concept space graph (CSG). A CSG is a
view of the concepts space distribution in the domain of a particular course.
A
concept space graph T(C, L) is a projection of a semantic net with vertices C
and links L where each vertex represents a concept and each link with weight l (i,
j) represents the semantics that concept cj is a prerequisite for
learning ci, where (ci, cj) Є C and the
relative importance of learning cj for learning ci is
given by the weight. Each vertex in T is
further labeled with self-weight value 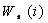 cumulative prerequisite set weight
cumulative prerequisite set weight 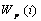 .
.
The self-weight 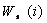 represents
the relative semantic importance of the root topic itself with respect to all
other prerequisites. The prerequisite weight
represents
the relative semantic importance of the root topic itself with respect to all
other prerequisites. The prerequisite weight 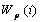 represents
the cumulative, relative semantic importance of the prerequisite topics to the
root node. Link weight is the strength of the prerequisite relationship between
the parent and the child. A CSG with root A is represented as T (A) in
Figure 2.5. For any node, co,
in the CSG, the sum of self-weight and
prerequisite weights and the sum of the prerequisite link weights to its child
node set
represents
the cumulative, relative semantic importance of the prerequisite topics to the
root node. Link weight is the strength of the prerequisite relationship between
the parent and the child. A CSG with root A is represented as T (A) in
Figure 2.5. For any node, co,
in the CSG, the sum of self-weight and
prerequisite weights and the sum of the prerequisite link weights to its child
node set 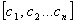 are
both always 1:
are
both always 1:
|
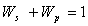
|
...(1)
|
|
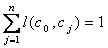
|
…(2)
|
2.4.1 Node Path Weight
It is the propagated prerequisite
effect of a subject node along a particular path to a root node. The notion of
node path weight is introduced to compute the effect a prerequisite node has on
a root node through a specific path. A single node, therefore, can have
different prerequisite effect on a root through different paths.
When
two concepts x0 and xt are connected through a path “p”
consisting of nodes given by the set 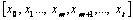 then the node path weight between these two
nodes is given by:
then the node path weight between these two
nodes is given by:
|
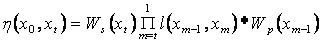
|
... (3)
|
The node path
weight for a node to itself is its self weight.
|
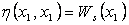
|
…(4)
|
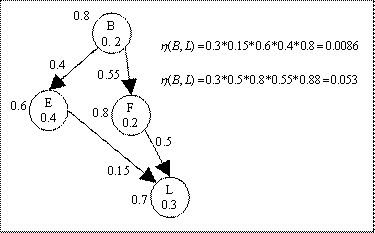
In the Figure 2.6 concept L is
connected to concept B through E and F. Therefore the prerequisite effect it
has on B is dependent on the prerequisite effect both E and F have on B
respectively. Node path weight calculates the prerequisite effect a node has on
another node. Therefore the factors of self weight of subject node and
prerequisite weights of all the nodes in the path are included in the formula.
From the node path weight
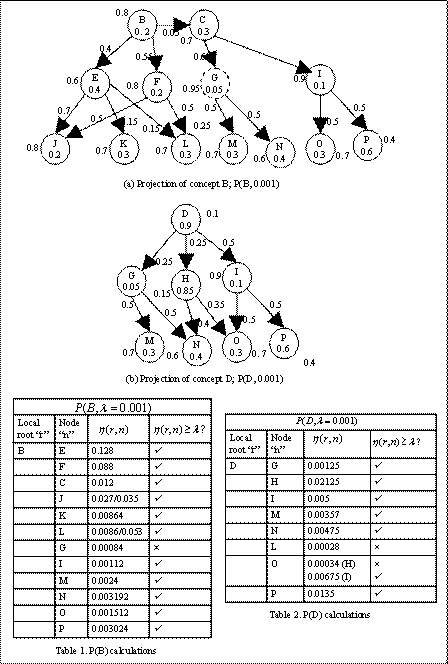
calculations we can see that L has a stronger prerequisite effect on B through
F rather than E. This is because, L is more important to F (0.5) than E (0.15),
prerequisite importance of L is more to F (0.8) than E (0.6) and subsequently F
(0.55) is more important to B than E (0.4). Thus node path weights takes into
consideration not only the singular effect a node has on its immediate parent
but also the combined prerequisite effect a node would have to a root, B in
this case, along a certain path.
2.4.2 Incident Path Weight
Incident path weight is same as node
path weight except that it does not include the factor of self weight of the
subject node. By doing this, we can compute the prerequisite effect the node
may have on a root node, excluding the factor of knowledge of the subject node.
It is defined as, the absolute prerequisite
cost required to reach the root node from a subject node.
|
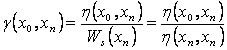
|
...(5)
|
From Figure 2.6, the incident path
weight calculations for paths between B and L are given by,
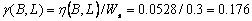
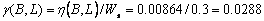
Educational resources and Test Problems
Most of the educational resources
today are not accompanied with metadata which makes it very difficult for
machine processing. For educational resources to be machine processable, they
have to be presented in the proper context [11]. In the last chapter we
described semantic representation standards and formal mechanism to represent
the concept space in detail. In this chapter
we look at resource space which is made
up of educational resources and the mapping between the resource space and the concept
space. One aspect of research in educational technology is the development
of technology in standards and practices for educational material research,
design, reuse, development, and reengineering. Though educational resources can
hardly replace the instructor, they can be very helpful in providing the
context of the subject matter. Therefore educational resources need to be
precise and intelligible.
A problem/question is one type of educational
resource. The commonly observed properties of testware are difficulty or
simplicity, breadth and depth of knowledge required to answer, relevance of the
question to the root topic, the semantic distance between the concepts tested,
ability of the question to test varying populations of students, applicability
of the topics taught to a problem, etc. While designing a test, an educator
always tries to come up with questions which have maximum coverage of desired
topics, diversity among the topics, good testing capabilities with respect to
student knowledge, relevance to the material taught, overall generality or
specificity. There are many other factors too; however the sub division of
those factors almost always leads to the above given basic properties of a good
question. It is important to understand these properties for better design and
reengineering of test problems. In this thesis, we attempt to visualize and
understand these properties of test problems by qualitative evaluation.
3.1.
Problem concept mapping
The mapping between the resource space and the concept space is called as the problem
concept mapping. All educational resources, including test problems are based
on a few selected concepts from the ontology. When an educator creates test
problems, although instinctively, there is a complex cognitive designing
process behind the whole task. The educator has a mental map of the concepts
taught in the course and depending on this map, the problems are composed. We
define a rudimentary version of this mental map in the form of course ontology.
The problem points to certain concepts from the ontology on which it is based.
This is called as the problem concept mapping. This is a highly cognitive
process which takes place in the human brain and needs a lot of research
work to be able
to explain it properly and formally. The research problem of mapping a problem
to concepts from ontology automatically is an extremely non-trivial problem
which involves research in natural language processing, knowledge
representation etc. We limit our research to using of the problem-concept
mapping in semantic evaluation. A mapping signifies the concepts which are used
to form the question, which also are the same concepts required to answer a
particular question.
The connection of the concepts to
the testware resource entity can be in the form of an “and” relationship or “or”
relationship. An “and” relationship
is used to define concepts which are imperative to answer the particular
problem. While the “or” relationship
defines an alternative between concepts to answer the problem. Example of
problem-concept mapping is shown in Figure 3.1. The dotted lines represent the
concepts which the problems maps to. The angle between the dotted lines is used
to represent “and” or “or” relations. If there is an “or” relation between two or more mapped
concepts then it means that, knowledge about any of the concepts is enough to
answer the problem. An “and”
relationship between two or more concepts means that, problem cannot be
answered without the knowledge of all “anded”
the concepts. From the figure 3.1, concept B and F are and’ed while concepts T,
K and F are or’ed.
These implicit relationships between
concepts can be effectively used in evaluating mathematics related problems. It
is observed that math problems generally involve a very well defined ontology
and numerous ways can be formulated to solve the problems. These solutions can
be conceptualized and mapped using or mapping. Whereas a more prose based
problem may require combined knowledge from various concepts to form a single solution.
These can be mapped as and concepts.
Test Problem Assessment
Educational resources must be
accessible and intelligible to varied groups of populations for consumption and
reuse. Currently there is no formal method for evaluating the utility of an
educational resource. We propose an assessment system which attempts to
evaluate an educational resource like test problem for its knowledge content
and complexity. The system is a framework based on assessment parameters. These
parameters can give guidelines for setting up a standard for test problem
assessment. This chapter describes in detail the assessment approach and
assessment parameters.
4.1.
Approach
The assessment process is essentially
a two step approach. The first main step is the extraction of the relevant
concepts from the CSG and is called as “CSG
extraction”. As seen in the previous chapter, each and every problem maps
to some concepts from the course ontology. The set of mapped concepts act as
the input to the assessment system hence the concept set has to be precise and
methodically selected. The mapping of the concepts signifies that to answer
that particular question, the set of mapped concepts are required. However, the
course ontology being a prerequisite relation based ontology, knowledge
required for understanding a concept, and consequently answering a question, is
represented as its prerequisite child concepts. Thus to comprehend a concept,
say A, all child node concepts of A have to be understood first, and to understand
all the child node concepts, their child node concepts have to be understood,
and so on. Therefore for better understanding of a concept, we have to go as far
down the ontology as possible. However, most ontologies are vast and there is
virtually no limit to how deep one can go in the ontology. Therefore there
needs to be a limit set for controlling the propagation. This limit is set by a
variable called as the threshold
coefficient and the process of extracting this relevant piece of sub graph,
called as the projection graph, is
called as CSG extraction. These
concepts are further explained in the later sections.
The second step in the assessment
process is applying algorithms to the individual projection graphs of each of
the mapped concepts to calculate the assessment parameters. In the subsequent
sections we define some assessment parameters which can help us in
understanding the relationships concepts have with a test problem, the
knowledge content required to answer a problem and properties of associations
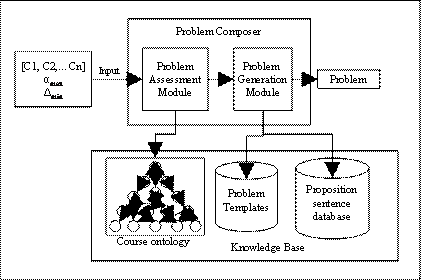
which concepts have with each other and the ontology root. Figure 4.1 shows the
assessment process. In the first step the CSG extraction module is given the
input i.e. the course ontology, the problem concept mapping and the threshold
coefficient value. Using these inputs the CSG extraction process outputs individual
concept projection graphs. In the next step the
projection
graphs and course ontology act an input to the assessment module which
calculates the values of assessment parameters.
4.2.
CSG Extraction
A generalized CSG
can be vast. Therefore we define a pruned sub-graph called as projection graph which cuts the
computation based on a limit on propagated semantic significance. The process
of selecting projection graph nodes from the Concept space graph is called as CSG extraction. There are quite a few
reasons to apply CSG extraction to ontology. The most important reason for CSG
extraction is computability. It is computationally very expensive to work on big
ontologies. Nowadays ontologies used range from thousands to millions of
concepts. Therefore processing the whole ontology is very expensive and also
doesn’t logically make sense. The concepts which the question maps to are
relatively very less as compared to the total number of concepts in the whole
ontology. More over, say if the mapped concepts are very distant from each
other in the ontology. This implies that the knowledge required to understand
these concepts is very diverse in the concept space. Therefore it would be a
squandering of computational resources to process the whole ontology instead of
just the relevant portions.
The concept space graph gives the
layout of the course in the concept space with a view of course organization,
involved concepts and the relations between the concepts. Examples of large
CSG’s include WordNet (150,000) an English language ontology, CYC (47,000
concepts, 30,000 assertions) a well known common sense knowledge mapping project
using ontology, LinKBase (1 million in English, 3 million in other languages) a
comprehensive medical/clinical ontology, Gene Ontology (now known as GO, over
19000 concepts) the genome mapping project, ThoughtTreasure (27,000 concepts,
51,000 assertions) another common sense mapping project, and so on. Thus
defining a workable area of ontology is of the utmost importance from the
perspective of semantic relevance and computability. The pruning is achieved by
introducing a variable called as the projection threshold coefficient (λ).
4.2.1 Threshold Coefficient (λ)
By varying the threshold coefficient
the size of the computable projection graph can be varied and thus the semantic
significance. Since the projection graph is a sub-graph of the concept space
graph, it is necessary to have pre-requisite weights for the leaf nodes too,
although most times the pre-requisite weight for the leaf nodes is zero.
Flexibility for optional pre-requisite weights for the leaf nodes allows the
CSG to be extensible and easily extractable for the projection.
Threshold coefficient is a kind of
virtual limit by which the size of the projection can be controlled. Greater
the coefficient more is the screening for the nodes to be added to the
projection and thus smaller is the graph. Less coefficient value means more
concepts will be included in the projection. The threshold coefficient can be
thought of as a parameter which can set the depth to which the topic has been
taught. If a topic is not taught in its entirety, a greater coefficient is
assigned so that the depth of the projection graph will be less. Conversely, if
a topic is pretty well covered, the value assigned to the threshold coefficient
is low, so that the projection graph for the concept is large, encompassing more
prerequisite concepts. By varying the threshold coefficient the exact semantic
relevance of the question to the whole graph can be computed, the result of
which is the projection graph, on which we operate. Threshold coefficient sets
the limit to how far one should go down the ontology.
4.2.2 Projection Graph
Given
a CSG T(C, L), with local root concept x0, and projection threshold
coefficient λ, a projection graph P (x0, λ) is defined as
a sub graph of T with root x0 and all nodes xt where
there is at least one path from x0 to xt in T such that
node path weights 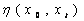 satisfies the condition:
satisfies the condition: 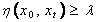 .
.
The projection
set consisting of nodes 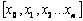 for a root concept x0 is
represented as,
for a root concept x0 is
represented as, 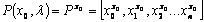 ;
where
;
where 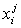 represents
the ith element of the projection set of node j.
represents
the ith element of the projection set of node j.
The projection graph points to that
area of the ontology of maximum semantic relevance. Consider an example CSG as
in Figure 2.5. We find the projection of the local root concepts B and D given
the threshold coefficient of λ=0.001. The projections and calculations are
shown in Figure 4.2 (a) and (b) and Tables 1 and 2. All nodes that satisfy the
condition of node path weights greater than threshold coefficient are included
in the projection. Nodes can have multiple paths to the root (J, L, and O). For
node J and L, both the path satisfies the condition, whereas for O only one
path satisfies the condition (O-I-D-A). Still, O is considered in the
projection of D, because it still wields some prerequisite effect on D through
one of the paths. If the condition for
the threshold coefficient is satisfied then the node is included in the
projection.
4.3.
Assessment parameters
The main objective of the assessment
parameters is to assess the overall knowledge content and the perceived
complexity of a test problem. In this section we describe three such assessment
parameters namely, coverage, diversity and conceptual distance.
4.3.1 Coverage (α)
The coverage of a question gives a quantitative
effect of the selected projection set on the knowledge required to answer a
particular question. Coverage of a concept is a direct indicator to the scope
of the question in context of the concept space of the course. Formally, “coverage
of a node x0 with respect to the root node r is defined as, the
product of the sum of the node path weights of all nodes in the projection set
P(x0, λ) for the concept x0 , and the incident path
weight γ (r, x0) from the root r”.
If the projection set for concept
node x0, P(x0, λ) is given by 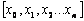 then the coverage for node x0 about
the ontology root r is defined as,
then the coverage for node x0 about
the ontology root r is defined as,
|
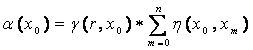
|
...(6)
|
where 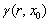 is the Incident Path Weight.
is the Incident Path Weight.
Total coverage
of multiple concepts in a problem given by set [C1, C2 … Cn]
is,
|
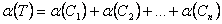
|
…(7)
|
In eq.6, it is seen that the main
factor contributing to the coverage is the summation of the node path weights
of all the nodes in the projection of a concept. From the definition of node
path weight, we know that it defines the semantic importance of a node to its
designated root. Therefore the summation of the node path weights of all the
nodes in the projection set gives the cumulative semantic importance of the node
in the projection graph on their respective mapped concept roots. The concepts
in the projection graph in turn are the concepts which are required to
understand a particular concept, controlled by the threshold coefficient. The
summation of the node path weights is the amount of knowledge required to
answer or rather understand a particular concept. The reason why the factor of
summation of node path weights is propagated to the ontology root using the
incident path weight is because the questions are asked about the ontology root
even though they do not directly point towards it.
Suppose a question tests concepts B
and D, Figure 4.2, calculate the coverage of the question given threshold
coefficient λ=0.001. The first step is to calculate the individual
projections of the concepts as seen in the projection calculation example. The
coverage of a concept is then the summation of the node path weights of all the
concepts in its projection, propagated to the ontology root. According to the formula,

4.3.2 Diversity (∆)
Diversity tests the extent of the knowledge
domain required to answer particular question. If the projections of some of
the mapped concepts overlap with each other, i.e. they have some concepts in
common; it means that they are less diverse as both indirectly depend upon some
common ground for their complete understanding. Whereas when no two concepts
are common it means that, the question has high diversity. Diversity is
calculated by measuring the effect of common and uncommon prerequisite concepts
from the projections of the mapped concepts. It is dependent on the uncommon
concepts rather than the common concepts because the disparate concepts attribute
the diversity to a question rather than the common concepts. Prerequisite
concepts in the projection sets of two or more of the mapped concepts, i.e. the
common concepts, only help in reinforcing the requirement for those concepts,
rather than contributing towards the diversity. A question has high diversity
value if the concepts it tests are distinct in the context of knowledge space.
Alternatively diversity measure can
be thought of as an inverse of similarity measure. There have been numerous
attempts to quantify the similarity between two concepts in ontology. Different
measures based on information content [36, 40, 42], distance [41], mutual
information, etc. have been studied. Our concept of diversity between two
concepts can give some insight into the similarity measures. It can be thought
of as an inverse similarity measure. We present a definition of diversity which
is not node based, link based or information based, but rather a knowledge
based approach which renders it uniqueness.
Diversity is formally defined as “the
ratio of summation of node path weights of all nodes in the non-overlapping set
to their respective roots, and the sum of the summation of node path weights of
all nodes in the overlap set and summation of node path weights of all nodes in
the non-overlap set.”
Consider a
question asks a set of concepts,  . The respective projection sets are given by,
. The respective projection sets are given by,
The
non-overlapping and overlapping sets are, 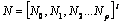 and
and 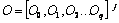 ,
where i and j are the local root parents of any element from N and O
respectively and
,
where i and j are the local root parents of any element from N and O
respectively and 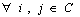 .
.
Cardinality
restriction:
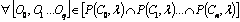 and
and 
Diversity is
given by,
|
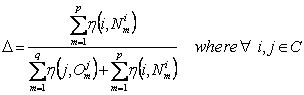
|
…(8)
|
Figure 4.3, shows the nodes in the
projections of B & D, and the shaded area shows the nodes in the
overlapping region. Diversity can be calculated by the means of the formula as,
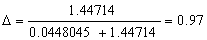
This means that
the diversity between concepts B and D is 97%. The concepts have high
diversity.
4.3.3 Conceptual Distance (δ)
Conceptual distance is a measure of
distance between two concepts with respect to the ontology root. According to
one of the definitions of similarity between nodes in taxonomy by Resnik, it is
the distance of the nodes from the subsuming parent [36]. Alternatively conceptual
distance measures the similarity between two concepts by quantifying the
distance of the concepts from the ontology root. Formally it is defined as “the log of inverse of the minimum value of incident
path weight (maximum value of threshold coefficient) which is required to
encompass all the mapped concepts from the root concept”.
The conceptual distance parameter is
designed in such a way that it should be sensitive to the depth of the
concepts. Hence it is a function of maximum threshold coefficient required to
cover all the nodes from the ontology root. Incident path weight (γ) of a
concept to the root is equivalent to the threshold coefficient (λ)
required to encompass the node. If question asks concept set  then the conceptual distance from the root
concept r is,
then the conceptual distance from the root
concept r is,
|
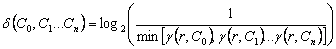
|
…(9)
|
Calculation of conceptual distance
for concept set [E, F, and M] is shown in Figure 4.4. Different types of arrows
represent the paths to the root from the respective nodes. In case on multiple
paths (M) the lowest values of incident path weight is considered.
Performance analysis and results
The performance analysis of assessment
parameters is two fold. In section 5.1 and 5.2 we analyze the assessment
parameters for their ability to be factors for reasoning about the perceived
complexity of problems and their knowledge content. In section 5.3, we analyze
the data qualitatively and make deducible inferences from the data.
For complexity analysis of assessment
parameters we use an extensive course ontology comprising of around 1500
concepts, for the course “Operating Systems” taught as graduate level course at
KSU. The ontology was created for the course by consulting the related
instructor and referring to standardized textbooks. The node weights and link
weights, which form an important constituent of the ontology, were assigned by
intuition and guidance from the course instructor. Concepts with more intrinsic
importance for understanding were assigned more self-weight and those which
depended on many other prerequisite concepts were assigned more prerequisite
weights. Consequently it is observed that concepts higher up in the ontology
have lower self-weights, and self-weights of nodes go on increasing further
down the ontology, reaching the maximum for leaf nodes. However, for the CSG to
be extensible, the leaf nodes are also allowed to have prerequisite weights in
case more prerequisite concepts are added later on. Keeping the ontology
extensible allows for inclusion of newer concepts, results, researches, etc.
adding to the inherent knowledge base, making the course ontology an ever
changing and improving repository of course knowledge. The link weights were
assigned based on the semantic importance and contribution of the child topic
to the understanding of the parent topic. If the understanding of the child
concept is detrimental to the understanding of parent concept than the other,
then it was assigned a greater link weight. Although by definition, the
summation of the link weights for a node should add up to 1, it is generally
not observed consistently. Most of the times, some space is left for the
inclusion of newer links for prerequisite concepts which are newly added or
already existing in the ontology. Again it is seen that higher up in the
ontology there is no need to actually leave this space, as the probability of
addition of newer links to higher level concepts is less than that to the
concepts lower in the ontology.
For the purpose of evaluation,
several problems were composed by the course instructor each mapping to some
concepts from the ontology. The problem concept mapping was provided by the
instructor in most cases with some inputs from students. These test problems
were administered by undergraduate and graduate students, the results from
which were used for the performance analysis. The answers to the problems were
graded by a minimum of three graders per question, and the averages of the
scores were considered for the analysis to remove anomalies. The coverage and
diversity of the concept set changes according to the changing values of λ
because they are the functions of node path weight which is relative to the
projection set, which in turn depends upon λ. Accordingly we experimented
with changing the threshold coefficient values and observing the result for
different projection graphs.
5.1.
Parameter performance against average score
In this section we evaluate the
performance of all the assessment parameters against the average score per
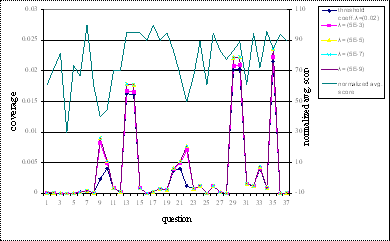
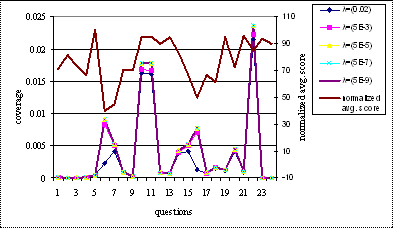
question. The coverage analysis for each question with varying threshold
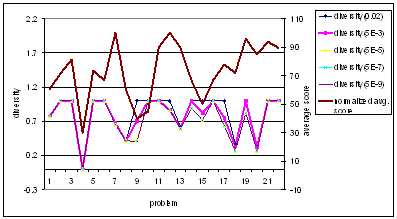
coefficient can be explained by the graph shown in Figure 5.1. It is observed
that the coverage has an inverse relationship with the average score. As the
average score increases the coverage for that particular question decreases and
vice versa. For all values of λ the coverage has the same relationship;
however this relationship becomes more and more evident with decreasing values
of λ. As λ decreases, the projection graph increases, thus increasing
the coverage values. Hence if the inverse correlation of the coverage graph
with average score graph is more for decreasing values of λ, we can infer
that more concepts are required to answer that particular question. Coverage
gives an approximation to the knowledge required to answer a particular
question. From the graph it is seen that most of the times, coverage is
inversely correlated to average score.
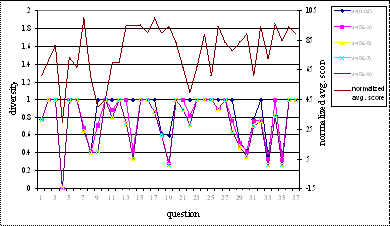
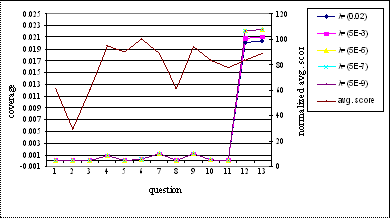
Diversity is also inversely
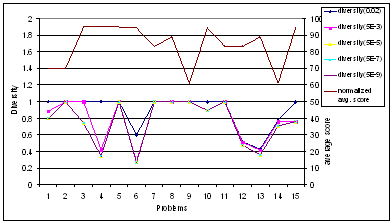
correlated to average score. Diversity graph characteristics are similar to coverage
graph, Figure 5.2. In the case of diversity it is observed that as the
threshold coefficient λ decreases, the diversity values for all the
questions also go on decreasing. This is because as the λ decreases the
projection set for each concept in the concept set increases. As the projection
set increases the probability of having more common concepts increases, thus
increasing the coverage of overlap set and decreasing the diversity. In some
cases however the diversity increases with decrease in λ. This happens
because, sometimes when the threshold coefficient decreases, the projection
obviously increases; however instead of having more overlapping nodes, the non
overlapping node set increases consequently increasing the diversity.
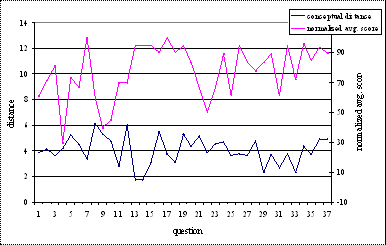
The performance of conceptual
distance versus average score is observed in Figure 5.3. Although not directly
dependent on projection graph, distance is also inversely correlated to average
score. This means that distance is a very good indicator of the similarity
between concepts. As the distance between two nodes decreases, the similarity
increases. As the similarity increases, the knowledge required to answer the
concepts decreases, consequently increasing the average points scored. As
conceptual distance is not a factor of projection graph, behavior in the graph
is constant for all threshold coefficients. Distance is a logarithmic function
as log gives the inverse behavior of
an exponential function, which is observed here. Similar to coverage and
diversity the conceptual distance is also inversely correlated to average score
with good correlation. As seen from the behavior of all three assessment
parameters, the average score has an inverse correlation with the parameters.
This means that the parameters are pretty good indicators of the perceived difficulty
of test problems.
5.2.
Correlation Analysis
In this section we study the
correlation between the parameters and average score for varying threshold
coefficient values. A high degree of inverse correlation is desired, so that as
average score increases, the values of the assessment parameters go down, and
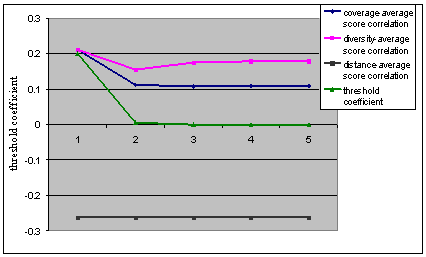
vice versa. From Figure 5.4 it is seen that as the threshold coefficient value
decreases, the correlation for coverage and diversity with average score also decreases
and then remains constant for lower values of threshold coefficient. The reason
for this behavior is that, when the threshold coefficient decreases, the
projection sets of the respective concepts increase as more and more nodes are
added. However the average score for a particular problem remains constant.
Hence if a problem has a high average score, it means that originally the
coverage and diversity for that problem was lower, but since the projection set
has increased, now their values have also increased. Due to this the
correlation between coverage and diversity and average score decreases.
Similarly, if a problem has low average score, it means that originally the
coverage and diversity for that problem were high, but since the projection has
increased, their values increase too. In this case the correlation has
decreased in the reverse direction. After some value of threshold coefficient
though, the projection set remains constant, and so does the correlation
between coverage and diversity and average score. The correlation between
conceptual distance and average score remains constant throughout because,
conceptual distance is independent of the projection graph and therefore the
threshold coefficient.
5.3.
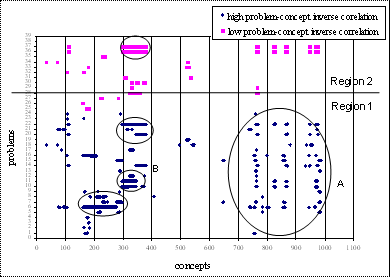
Qualitative Data Analysis
5.3.1 Test
based analysis
Though most of the times coverage
and diversity values are inversely proportional to average score, it is
important to observe and measure the percentage variation to draw inferences.
Figure 5.5 shows the distribution of
concepts according to the concept mapping of the problems according to the tests.
Problems 1-6 are in test a, 7-12, 13-18, 19-37 are in tests b, c and d
respectively. A simple scatter plot of question-concept can give a lot of
information. Observations and Inferences:
- Questions 13, 14, and 29, 30, 33, and 35 ask almost
similar concepts. Out of these 13, 14, 33 and 35 have good inverse
correlation with average score, but 29 and 30 don’t. This implies that
these questions have some implicit factors other than the mapped concepts which
made them difficult, which in turn decreased the average score
correlation.
- Most questions are based on or relate to concepts
from 100-400 and 750-1000. That means that most of the tests were based on
that part of the ontology. This inference has a very interesting
implication. It means that, the instructor chose to set the problems only
on select topics from the course ontology. The obvious inference is that;
those were the only topics covered in the course from the ontology. The
exact portions of the ontology which were taught and tested can be pointed
out using this analysis.
- Test “a”
asks concepts only around 200, but the distribution of concepts increases
with the tests. As more and more topics are taught from the ontology, tests
are increasingly based on more concepts than the previous.
- There is a small clustering of concepts followed by a
slightly bigger clustering, between concepts 50-250. Since the concepts
were numbered levels wise it means that the small cluster are the mapped
concepts, while the rod is the projection of the mapped concepts. This behavior
is seen through out the graph. Clustering following smaller clustering usually
means projections of mapped concepts.
5.3.2 Correlation based analysis
In this analysis, we separate out
the problems which do not show good correlation with average score from those
which do. In the context of assessment parameters and average score, an inverse
correlation between the two is considered good, and vice versa. These problems are
then analyzed to make intuitive inferences as to why the observed correlation
is good or bad. In Figures 5.6, 5.8 most of the problems have high inverse
correlation with average score, while in Figures 5.7, 5.9 most have very low inverse
correlation as seen in the plots. For correlation based qualitative data
analysis, the problems which have an inverse correlation between coverage and
average score were separated out from those which don’t.
On carefully observing the set of
concepts to which these problems map to, it is seen that there are surprisingly
high number of common concepts and among the problems with good and bad
correlation. It is important to note here that, rather than just considering
the mapped concepts, the projections of the mapped concepts were considered as
they would give a better understanding of the whole set of prerequisite
concepts required to answer the question. Figure 5.10 shows the problem-concept
distribution separated for the questions with high inverse and low inverse
correlation between coverage/diversity and average score. Interesting
inferences can be made by observing the graph.
- In area A there is similar concept distribution
across problems with a good correlation. From this we can infer that
students know those concepts well, or the problems based on these concepts
were fairly easy to answer, or these concepts are intrinsically easier to
understand and answer. However it is seen that, for the same concepts,
there are a few problems (36-37) which have bad correlation with average
score. This again could mean that these problems were harder because of
some other parameters, or these problems required knowledge from out of
the scope of this ontology. If similar clustering behavior is observed in problems
which have bad correlation with average score, then it can almost
conclusively be said that, those concepts or that part of the ontology
needs more attention i.e. either the course instructor should teach the
concepts again, or if the concepts are intrinsically difficult to
understand then they should be somehow be simplified for the students.
- It is observed that in problems with low inverse
correlation, concepts are more dispersed (as in, not clustered) around the
ontology as compared to those with high inverse correlation.
- The small clusters in area B, mean that problems usually
ask concepts near and around a primary concept. These small clustered
concepts mostly are those concepts which come in the primary concepts projection
itself. Two small clusters near each other mean two primary concepts
projections which are very near to each other.
- Concepts around 200-400 and 750-1000 are frequently
asked among the questions with high and low inverse correlation equally.
This means that the tests were based on those concepts and not
specifically on others and the concepts which appear scattered around the
plot are those which are needed to answer the specific problem. The
concepts which do not form the part of the cluster are most definitely
concepts, which are distant from the primary concept, however still
necessary to answer the particular problem completely.
- Another interesting observation is that, in the
questions which have low inverse correlation, the projections of the primary
concepts are very small (dots) compared to those in the questions with
high inverse correlation (rods). This means that even though the same
concepts are asked, with smaller or bigger set of prerequisite concepts
required to answer it, the question composition itself has some properties
other than the asked concepts which attribute difficulty/simplicity to it.
In this vein, a lot of information can be gathered and inferences can be
made.
Applications and Future Work
The assessment framework can be
intuitively applied to a number of applications. It provides a system for
qualitative assessment of a test problem and gives values of desired coverage,
diversity and conceptual distance to work with. To enable automatic assessment
of any kind, it is important to have numerical values to realize intangible
aspects of a problem like its difficulty. We present a few applications where
the assessment framework can be employed. Much of the formal development of
these applications is a future work. In this thesis we simply put forth the
ideas for possible applications.
6.1.
Automatic test generation
We propose an algorithm which can select
problems from a database with specific difficulty values and compose a test
with desired complexity and desired area of testing. Most of the tests composed
by educators today are composed manually. Also the final product, the test, is
not associated with any characteristics like difficulty and area of testing. It
is important to know these characteristics of a test to be able to more
efficiently teach, grade and analyze. The task of selecting a proper set of
problems, which is complete in coverage and precise in difficulty, is a
mechanical task which can be put in an algorithm. Difficulty values for
problems can be calculated using function of coverage, diversity and conceptual
distance. The output is a test with a specific set of problems which cover
certain topics from the area and also amount to a specific level of difficulty.
The test composition algorithm is a minimalist binary knapsack algorithm, where
in the composer has to select questions and also weigh the selection against
difficulty value constraint. The input to the algorithm is a set of concepts on
which the test is based. The problems in the database have a difficulty value
and problem concept mapping. The algorithm selects problems from the database
depending on the problem concept mapping and difficulty values until all the
desired concepts are included in the test and a specific difficulty value is
met.
This
algorithm can be used to create variations of difficulty for a test, a
relatively hard test, a relatively easy test and a test with difficulty
centered on a specific value. If the algorithm starts by selecting only the
more difficult or lesser difficult problems form the test we can ultimately
compose a test which is harder or easier respectively. To compose a test around
a specific difficulty the algorithm can be easily modified to select a question
with difficulty value as close to the desired difficulty value as possible,
instead of selecting the first question from the question set every time.
6.2.
Semantic Problem Composition
To design a question we should first
be able to properly evaluate the perceived difficulty of a question. Semantic problem
composition uses the assessment framework to compose a problem automatically. A
problem composer must be aware of the difficulty/ease of a problem, the student
knowledge/prerequisite and understanding, relevancy of the problem to the
topics being taught, student evaluation capability of the problem, etc. Also
the problems selected for the test have various properties like hardness/ease,
time required to answer, mathematical complexity, the length and breadth of the
topics it covers, the relevancy of the topics, etc. Most of these considerations
can be accounted for in the problem assessment parameters. The architecture of
the composer
is shown in Figure 6.1. The two main
modules are the problem assessment module and the problem generation modules. The
inputs to the problem assessment module are the desired set of concepts, the
desired maximum coverage and minimum diversity. Based on these concepts and the
values, the algorithm finds out the projections of the concepts and thus the
amount of knowledge required to compose the problem with the constraints on
coverage and diversity. All these selected concepts then act as input to the
problem generation module. This module puts the concepts in fixed problem
templates created by analyzing a variety of problems, and puts them into
sentences using propositions from the database. The final product is a problem
which requires a specific set of concepts to answer and with a desired coverage
and diversity, composed using problem templates and sentence construction algorithms.
6.3.
Semantic Grader
If the cognitive process of problem
composition can be automated with the necessary knowledge support given by course
ontologies, then we can have an efficient system that can not only create
courses and tests automatically considering various factors but also evaluate
the tests. At present the process of grading or assessment of answers is mostly
manual barring a few good exceptions. Automatic grading of answers has been an
interesting research problem for a long time in the educational technology
research community. Most of the work in automatic grading is in grading
programming assignments. One of the prominent examples is KASSANDRA [48]. E-rater
at ETS has experimented with automated evaluation of answer [47]. In this
thesis we propose an approach for automatic grading of answers irrespective of
the format of the answer. We propose an initial architecture for the system and
plan to develop a completely automated system for grading answers in the
future.
From, Chapter 2 and 4 we understand
that problems can be mapped to concepts from the ontology. Based on these
mapped concepts, we generate projection graphs for the individual concepts, and
calculate the assessment parameters based on them. With the same reasoning, we
can apply a CSG extraction procedure to the solutions. A grader initially
points out the concepts from the ontology which the solution includes. If we
know this, “solution concept mapping”,
we can apply the same procedures for CSG extraction to the solution too and
obtain a cumulative projection graph of the solution. Once we have the
cumulative projection graphs for the problem and the solution, we can apply
graph comparison algorithms to determine parameters which can guide through the
process on grading of answers.
This method of grading is more
comprehensive and non-trivial. The grading is more knowledge oriented. Once the
solution projection graph (SPG) is obtained, the exact concepts contained in
the solution can be pointed out and hence the knowledge gained by the student.
The SPG can contain more concepts or fewer concepts than the required set,
governed by the PPG, and the solution is graded accordingly. Figure 6.2 shows
the working of the semantic grader. The problem concept mapping, solution
concept mapping and course ontology act as the preliminary inputs to the CSG
extraction module. The outputs of this stage, i.e. SPG and PPG then act as
input to the module which applies graph comparison algorithms on them to
finally give parameters needed for grading. Based on these parameters the final
grade is computed. The parameters give an estimation of how different are the
SPG and PPG, does the SPG contain any extra concepts which are not needed to
answer but are still relevant to the question, are there any new relationships
between the concepts in the SPG which are significant, etc. As a part of the
future work we propose to implement this system for a more complete course
ontology based semantic grader.
Conclusion
In computer aided automated design
of educational resources, specifically test problems, a backend system for the
assessment of these test problems is an absolute must. We propose a system for
the assessment of test problems based on a few synthetic parameters. The
knowledge support for the system is provided by course ontology. Course
ontology is a formal description of the concept knowledge space associated with
a course. It is described in a specifically customized language, called as
Course Ontology Description Language and is written in OWL. The course ontology
representation is expressible and computable at the same time. We present a
novel approach to extract relevant information from course ontology depending
on the desired semantic significance. Using this method computation cost for
processing ontological information can be greatly reduced. Finally we propose
some parameters for evaluating the knowledge content and the complexity of a
test problem using the concept knowledge from the course ontology. The
parameters are formulaic and derived from real world understanding of the
factors which attribute complexity to a problem like, coverage, diversity and conceptual
distance. The parameters are then tested in the real world scenario of tests,
and it is observed that they perform very well. These parameters maybe used for
the standardization of test-ware which can further the development of
fundamental applications in reuse and engineering of digital content on the
web. Interesting observations are made in regards to the information which can
be extracted and used from these ontologies. The assessment framework can be
employed to create automatic design and evaluation systems like test
composition, problem composition, semantic grading etc. Further more the
ontology expression language can be extended to incorporate more information
from the course, and thus try to infer more interesting results.
|
[1]
|
Javed I. Khan, Manas Hardas, Yongbin Ma, A Study of Problem Difficulty Evaluation
for Semantic Network Ontology Based Intelligent Courseware Sharing. WI,
pp. 426-429, the 2005 IEEE/WIC/ACM International Conference on Web
Intelligence (WI'05), 2005.
|
|
[2]
|
Laura M.
Bartolo, Sharon C.
Glotzer, Javed I. Khan, Adam C. Powell, Donald R. Sadoway, Kenneth M.
Anderson, James A. Warren, Vinod Tewary, Cathy S. Lowe, Cecilia Robinson: The materials digital library: MatDL.org.
398
|
|
[3]
|
Materials Science Digital Library,
MATDL. http://matdl.org/fez/index.php
|
|
[4]
|
Professional Development Center, ACM http://pd.acm.org/
|
|
[5]
|
Universia. http://mit.ocw.universia.net/
|
|
[6]
|
MIT Open Course Ware http://ocw.mit.edu/OcwWeb/index.htm
|
|
[7]
|
Chinese Open Resources for Education, Core.
http://www.core.org.cn/en/index.htm
|
|
[8]
|
Center for Open and Sustainable
Learning, COSL.http://cosl.usu.edu/
|
|
[9]
|
2004 MIT OCW Program Evaluation
Findings Report (June 2006). http://ocw.mit.edu/NR/rdonlyres/FA49E066-B838-4985-B548-F85C40B538B8/0/05_Prog_Eval_Report_Final.pdf
|
|
[10]
|
National Science Digital Library,
NSDL. http://nsdl.org/
|
|
[11]
|
Jaakkola, T., Nihamo, L., Digital Learning Materials do not Possess
knowledge: Making critical distinction between information and knowledge when
designing digital learning materials for education International
Standards Organization, Versailles, 2003.
|
|
[12]
|
Oliveira, J.P., Muñoz, L.S., Freitas,
V.,
Marçal, V.P., Gasparini, I.,
Amaral, M.A. (2003). Adapt Web: an
Adaptive Web-based Courseware (III ANNUAL ARIADNE CONFERENCE, 2003, Leuven. Katholieke Universiteit Leuven, Belgium.
|
|
[13]
|
Silva,
L., Oliveira, J.P., (2004). Adaptive Web Based Courseware
Development using Metadata Standards and Ontologies. AH 2004, Eindhoven.
|
|
[14]
|
Kuo, R., Lien, W.-P., Chang, M., Heh,
J.-S., Analyzing problem difficulty
based on neural networks and knowledge maps. International Conference on
Advanced Learning Technologies, 2004, Education Technology and Society,
7(20), 42-50.
|
|
[15]
|
Rita Kuo, Wei-Peng Lien, Maiga Chang,
Jia-Sheng Heh, Difficulty Analysis for
Learners in Problem Solving Process Based on the Knowledge Map.
International Conference on Advanced Learning Technologies, 2003, 386-387.
|
|
[16]
|
Lee, F.-L, Heyworth, R., Problem complexity: A measure of problem
difficulty in algebra by using computer. Education Journal Vol 28, No.1,
2000.
|
|
[17]
|
Li, T and S E Sambasivam. Question Difficulty Assessment in Intelligent Tutor Systems for
Computer Architecture. In The Proceedings of ISECON 2003, v 20
(San
Diego): §4112. ISSN: 1542-7382. (Also appears in Information Systems
Education Journal 1: (51). ISSN: 1545-679X.)
|
|
[18]
|
Edmondson, K., Concept mapping for Development of Medical Curricula. Presented
at the annual meeting of the American Educational Research Association
(Atlanta, GA, April 12-16, 1993). 37p.
|
|
[19]
|
Heinze-Fry, J., & Novak, J. D.,
(1990) Concept mapping brings long term
movement toward meaningful learning. Science Education 74(4), 461-472.
|
|
[20]
|
Novak, J. D., (1991) Clarify with concepts. The Science
Teacher 58(7), 45-49.
|
|
[21]
|
Novak, J. D., (1990) Concept mapping: A useful tool for science
education. Journal of research in Science Teaching 27(10), 937-949.
|
|
[22]
|
Knowledge
Representation Issues,
Artificial Intelligence, Elaine Rich and Kevin Knight, 2nd ed. 1991,
McGraw-Hill Inc. 105 pp.
|
|
[23]
|
Thornton, C. (1995). Measuring the difficulty of specific
learning problems. Connection Science, 7, No. 1 (pp. 81-92).
|
|
[24]
|
Heffernan,
N. T. & Koedinger, K. R. (1998). A developmental model
for algebra symbolization: The results of a difficulty factors assessment. In Proceedings of the Twentieth
Annual Conference of the Cognitive Science Society, (pp. 484-489). Hillsdale, NJ: Erlbaum.
|
|
[25]
|
Croteau, E., Heffernan, N. T. & Koedinger, K. R. Why Are Algebra Word Problems Difficult? Using Tutorial Log Files and
the Power Law of Learning to Select the Best Fitting Cognitive Model. 7th
Annual Intelligent Tutoring Systems Conference, Maceio, Brazil, 2004.
|
|
[26]
|
Heffernan, N. T., & Koedinger, K.
R.(1997) The composition effect in
symbolizing: the role of symbol production versus text comprehension. In
Proceeding of the Nineteenth Annual Conference of the Cognitive Science
Society (pp. 307-312). Hillsdale, NJ: Lawrence Erlbaum Associates.
|
|
[27]
|
Koedinger, K. R. & Nathan, M. J. The real story behind problems: Effects of
representations on quantitative reasoning. Journal of Cognitive
Psychology, 1999.
|
|
[28]
|
Draft Standard for
Learning Object Metadata,
15 July, 2002, Technical Editor: Erik Duval. http://ltsc.ieee.org/wg12/files/LOM_1484_12_1_v1_Final_Draft.pdf
|
|
[29]
|
OWL
Web Ontology Language Guide, Michael K. Smith, Chris Welty, and Deborah L. McGuinness, Editors,
W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-owl-guide-20040210/ . Latest version available
at http://www.w3.org/TR/owl-guide/.
|
|
[30]
|
OWL
Web Ontology Language Reference, Mike Dean and Guus Schreiber, Editors, W3C Recommendation, 10
February 2004,
http://www.w3.org/TR/2004/REC-owl-ref-20040210/. Latest version available at
http://www.w3.org/TR/owl-ref/
|
|
[31]
|
OWL
Web Ontology Language Overview, Deborah L. McGuinness and Frank van Harmelen, Editors, W3C
Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-owl-features-20040210/. Latest version
available at http://www.w3.org/TR/owl-features/
|
|
[32]
|
OWL
Web Ontology Language Semantics and Abstract Syntax, Peter F. Patel-Schneider, Patrick
Hayes, and Ian Horrocks, Editors, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-owl-semantics-20040210/ . Latest version
available at http://www.w3.org/TR/owl-semantics/
|
|
[33]
|
Defining
N-ary Relations on the Semantic Web. W3C Working Group Note 12 April 2006. Editors: Natasha Noy, Stanford University, Alan Rector, University of Manchester. Contributors: Pat Hayes, IHMC, Chris
Welty, IBM Research. Latest version: http://www.w3.org/TR/swbp-n-aryRelations
|
|
[34]
|
Representing
Classes As Property Values on the Semantic Web, W3C Working Group Note 5 April
2005.Editor: Natasha Noy, Stanford University, Contributors: Michael Uschold,
Boeing, Chris Welty, IBM Research. Latest version: http://www.w3.org/TR/swbp-classes-as-values
|
|
[35]
|
RDF
Vocabulary Description Language 1.0: RDF Schema, Dan Brickley and R.V. Guha, Editors.
W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-schema-20040210/ .
Latest version available at http://www.w3.org/TR/rdf-schema/.
|
|
[36]
|
Resnik, P.: Using information content to evaluate semantic similarity in taxonomy.
In Mellish, C., ed.: Proceedings of the 14th International Joint Conference
on Artificial Intelligence, Morgan Kaufmann, San Francisco (1995) 448--453
|
|
[37]
|
C.E. Shannon. A Mathematical Theory of Communication. Bell Systems Technical
Journal, 27:379-423, 623-656, 1948.
|
|
[38]
|
Taricani, E. M. & Clariana, R. B.
(2006). A technique for automatically
scoring open-ended concept maps. Educational Technology Research and
Development, 54, 61-78.
|
|
[39]
|
Waikit Koh and Lik Mui, An Information Theoretic Approach to
Ontology-based Interest Matching, IJCAI'2001 Workshop on Ontology
Learning, Proceedings of the Second Workshop on Ontology Learning OL'2001,
Seattle, USA, August 4, 2001 .
|
|
[40]
|
D. Lin, 1998. An Information-Theoretic Definition of Similarity. Proceedings of
International Conference on Machine Learning, Madison, Wisconsin, July, 1998.
|
|
[41]
|
Gabriela Polcicova and Pavol Navrat, Semantic Similarity in Content-Based
Filtering, Advances in Databases and Information Systems, 6th East
European Conference, ADBIS 2002, Bratislava, Slovakia, September 8-11, 2002,
Proceedings. Lecture Notes in Computer Science 2435 Springer 2002, pp 80-85 ISBN
3-540-44138-7
|
|
[42]
|
Carl Van Buggenhout, Werner Ceusters, A novel view of information content of
concepts in a large ontology and a view on the structure and the quality of
the ontology, International Journal of Medical Informatics (2005) 74,
125-132.
|
|
[43]
|
Wenger, E. (1987). Artificial Intelligence and Tutoring
Systems, Morgan Kaufmann.
|
|
[44]
|
Cummins,
D. D., Kintsch, W., Reusser, K. & Weimer, R. (1988). The
role of understanding in solving word problems. Cognitive Psychology, 20, 405-438.
|
|
[45]
|
R. Davis, H. Shrobe, and P. Szolovits.,
What is a Knowledge Representation?,
AI Magazine, 14(1):17-33, 1993
|
|
[46]
|
T. R. Gruber. A translation approach to portable ontologies. Knowledge Acquisition,
5(2):199-220, 1993
|
|
[47]
|
Burstein, J., Chodorow, M., &
Leacock, C. (2004). Automated essay
evaluation: The Criterion online writing service. AI Magazine, 25(3),
27-36.
|
|
[48]
|
Urs von Matt. Kassandra: the automatic grading system. SIGCUE, (22):26--40,
1994.
|
![]() cumulative prerequisite set weight
cumulative prerequisite set weight ![]() .
.
![]() represents
the relative semantic importance of the root topic itself with respect to all
other prerequisites. The prerequisite weight
represents
the relative semantic importance of the root topic itself with respect to all
other prerequisites. The prerequisite weight ![]() represents
the cumulative, relative semantic importance of the prerequisite topics to the
root node. Link weight is the strength of the prerequisite relationship between
the parent and the child. A
represents
the cumulative, relative semantic importance of the prerequisite topics to the
root node. Link weight is the strength of the prerequisite relationship between
the parent and the child. A ![]() are
both always 1:
are
both always 1:![]() then the node path weight between these two
nodes is given by:
then the node path weight between these two
nodes is given by:![]()
![]()