

Author: Alok Prakash
email:
aprakash@cs.kent.edu,
homepage: http://www.cs.kent.edu/~aprakash
Prepared for Prof. Javed I. Khan
Department of Computer Science, Kent State University
Date: May 2006
Abstract: As Peer-to-Peer (P2P) networks grow in popularity, the ease, accuracy and efficiency of search for resources stored in the network has become one of the determining factors in the adaptation of any P2P network. Different P2P networks use different overlay schemes and thus a same model of search is not going to be efficient in all the P2P networks. Some of the search techniques are very simple and straightforward while others employ complex techniques, all leading to different levels of efficiency. In this survey paper, I will be focusing on some of the advance search techniques used in P2P network and discuss their working, suitability and possible advantages and disadvantages.
[Keywords]: Peer-to-Peer Search, Range Query, Random Walks, Percolation Search, Hierarchical DHT
Other Surveys on Internetwork-based Applications
Back to Javed I. Khan's Home Page
A P2P network is a network of peers where, ideally, there is no central authority. Peers can join and leave the network at any time, at their will. All the peers in the network contribute resources, in form of storage space, bandwidth etc. It is a network based on collaboration, so each peer stores some data. The distribution of data can be random, thus the data stored in a P2P network is usually scattered across a large number of peers. This architecture demands a very efficient search technique for the retrieval of data from the P2P networks.
A search technique for a P2P network needs to fulfill some criteria in order to be used widely as an established technique. Some of these issues are absolute necessities while some others can be classifies as 'good to have'. As newer P2P schemes are being developed, the associated search techniques are also improving, though a lot remains to be accomplished. Some of these challenges, both solved and unsolved, are -
There are many search techniques available to search for data in P2P networks. These search techniques could be classified in many ways. We will be classifying the search techniques into two groups -
The conventional search technique used in the P2P networks is a broadcast search and is also known as flooding. This technique is widely used in unstructured P2P networks like Gnutella. In this type of search each peer receives and processes every single query. Every query has a unique identifier associated with it. When any peer gets a query, it checks the unique identifier of the query to verify if it has already processed the query. This is done to make sure that every peer processes a query no more than once. After processing the query (or skipping processing), the peer forwards the query to all the peers in its routing table.
This is not the most efficient method of searching as in most cases only a few peers will have the result and all the other peers would be performing redundant query processing. This is wasteful in terms of bandwidth for the network and processing power in case of the individual peers.
There are some advance search techniques that can be applied to the P2P networks. These techniques are more efficient than flooding, some in terms of processing required while others in terms of bandwidth costs. These are specialized search techniques and might provide the best performance in only selective cases. In this paper, we will be discussing the following advance search methods -
We also discuss Hierarchical DHT in this survey as it presents a very interesting routing and search mechanism.
Here we discuss some of the concepts that would help understanding the techniques discussed in this survey better.
Random walk, also known as Markov chain and "drunkard's walk", is a path constructed by taking successive steps in random directions.
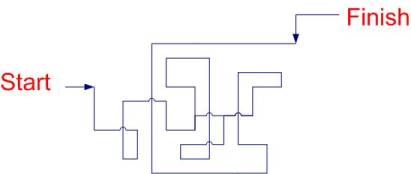 |
| Figure 1: A random walk |
The Markov property means the system is memory-less i.e. previous states are irrelevant for predicting the subsequent states. The conditional probability distribution of the future state, given the present and past states, is a function of the present state alone. Thus the path constructed by a random walk follows the following properties -
There is a starting point.
The distance from one point in the path to the next is a constant.
The direction from one point in the path to the next is chosen at random, and no direction is more probable than another.
In mathematics, percolation theory describes the behavior of connected clusters in a random graph. Percolation theory can be used to deal with degree of connectivity of a graph.
If 'p' is a parameter that defines the average degree of connectivity between various sub-units of some arbitrary system, then the percolation threshold is that value of 'p' at which there is no longer an unbroken path from one side of the system to the other.
Percolation can be further categorized as -
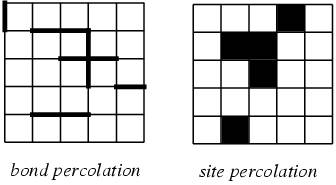 |
| Figure 2: Bond and Site percolation. Image courtesy MathWorld |
We will be looking at the bond percolation methods for search in P2P networks.
Distributed Hash Table networks traditionally follow a pure flat design. The flat design provides a uniform distribution of peers thus ensuring scalability and load balancing in the overlay network.
Hierarchical DHT (HDHT), on the other hand, is a class of DHT that don't follow the pure flat design. They have a combination of flat and hierarchical design. There are broadly two types of HDHTs -
We will be concentrating on Cyclone[ 4 ], which is a Horizontal HDHT.
These are the queries that ask for a dataset between a given range. This type of query has an upper bound and a lower bound. This technique could drastically reduce the number of queries and all the cost associated with it when the user is looking for results between a range and hence there is a possibility of more than one possible result.
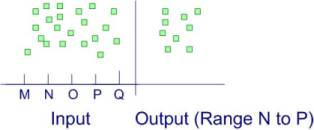 |
| Figure 3: Range Query |
Search using random walk technique can be used effectively in unstructured (non DHT) P2P networks like gnutella. Christos Gkantsidis et. al. propose in [2] that search using random walk technique in unstructured P2P networks can be better than flooding, which is the primary and most used search techniques for unstructured P2P networks, if the following two conditions are valid -
The notion of peers forming the cluster is based on the intuition that a peer knows and forms bond with other peers who share the same interests. This theory is yet to be proven but the hypothesis seems to be correct. The reason for its correctness is that each peer keeps a cache of other peers and picks its neighbors from its cache that is populated by the addresses of peers that answered previous queries. Thus a virtual cluster is formed where the members share similar interest and hence a search conducted by any peer is likely to be more successful in the cluster than in the rest of the network. Figure (4) below illustrates this behavior, where peers with similar musical tastes have formed virtual clusters.
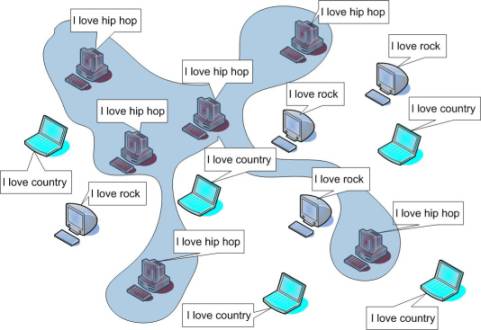 |
| Figure 4: Peers sharing similar interests form a virtual cluster (Click on image to expand) |
This is where random walk can be more useful than flooding. While searching, flooding will not take the clustering into consideration. Random walk, on the other hand, would choose the peer for the next hop from the address cache of the search initiating peer thus searching the cluster first. Since the chances of search being successful is higher in the cluster, hence the probability of random walk returning with results in lesser number of hops would be much higher than flooding.
When a peer issues a request, the user (or, the system on behalf of the user) re-issues the same request multiple times hoping to locate more peers with results. In this scenario, flooding, that has no randomness in its method, would mostly come back with the already known results, given that the topology remains largely unchanged between the successive requests.
But random walks, for the same number of messages, follow totally different trajectories and thus have better chances to discover new sources.
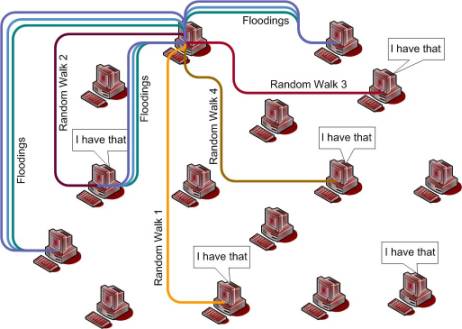 |
| Figure 5: Floodings return with same result while consecutive random walk goes to different peer (Click on image to expand) |
Figure (5) shows the case of repeat searches. In this figure we see that multiple flooding attempts return with same set of results, while random walk returns with different result.
Percolation search technique can be an effective way of searching in unstructured P2P networks that have Power Law (PL) distribution. In a PL distributed networks there are a very few peers with very high degree, i.e. they are very highly connected, and most of the peers have low degree distribution. A peer is considered to be highly connected if its degree is >= the max degree in the network/2. The percolation search algorithm takes advantage of the network being PL distributed by making the query reach the high degree peers. Since these high degree peers are highly connected, the probability of query being answered at these peers is very high. Nima S, et. al. propose in [1] that the whole process can be conducted in three distinct phases - content list implantation, query implantation and percolation search.
Content list implantation takes place when the peer joins the network. The peer in this phase caches or implants its list of contents on some other peers in the network and hence the name of the phase. Each peer does this by taking a random walk through its peers, starting from itself, and duplicating its content list at each step. The random walk is of size O(logN) where N is the number of peers in the network. Thus the total number of contents is O(N logN) and the average cache size is O(logN). This process ensures that a pointer to any content is available at least one highly connected peer.
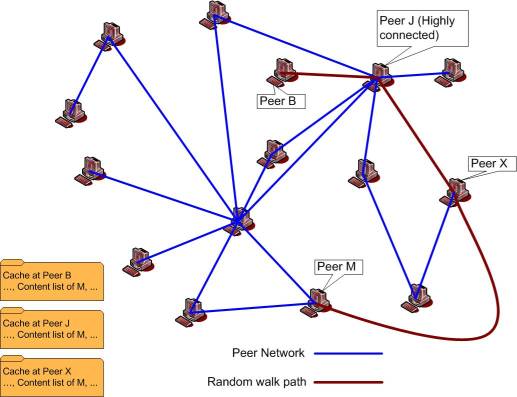 |
| Figure 6: An example showing the content list implantation of peer M (Click on image to expand) |
Figure (6) shows the content list implantation process for peer 'M'. It chooses a path at random and reaches peer 'X' after the random walk. It caches its content list at peer 'X' and continues the random walk. In the process it also saves its content list at peer 'J' which is a highly connected peer. This is the important part of the content list implantation.
The query implantation phase is the first phase that takes place while the requesting peer issues a query. The requesting peer does a random walk of size O(logN) and at each step 'implants' the query at that peer. This way when the requester and all the peers that have the query implanted on them would be taking part in the search. The main aim of this step is to implant the query on at least one highly connected peer. If the query gets implanted on any high degree peer then the probability of search being successful within minimum hops becomes high. This process could be visualized with the help of figure (6) if we replace the content link implantation process with query implantation process.
This is the phase where lookup for the data key being searched is performed. Before reaching this phase content list cache must be in place and query must have been implanted. When this phase begins then all the peers that have this particular query implanted on them start a probabilistic broadcast search. While doing the broadcast search any peer looks up it routing table and chooses neighbors and sends the query to them probabilistically. This is a case of percolation problem and that's why the name. The probability with which any peer sends the query to its neighbor is calculated by the following equation -
Probability of query being sent to a neighbor = percolation threshold / exponent of PL distribution
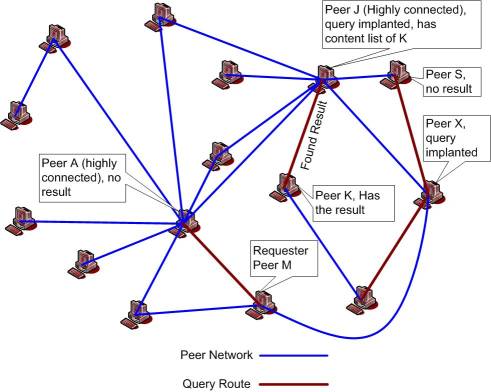 |
| Figure 7: An example showing the bond percolation search phase (Click on image to expand) |
The example in figure (7) shows a percolation search. Peer 'M' is the requester and it has implanted the query on peers 'J' and 'X'. All three peers 'M', 'J' and 'X' choose the neighbor whom they would be sending the query probabilistically, but not to all the neighbors in their routing table. Peer 'K' has the result and peer 'J' knows this because it has the content list of 'K' implanted on it. 'J' queries 'K' and 'K' replies with the result.
In an unstructured P2P network with PL distribution, a successful search is almost guaranteed if the exponent of PL distribution is close to 2 and the percolation threshold is close to (logN)/(Square-root of N), where N is the number of peers in the network.
As discussed above, range queries search for a range of dataset. Range queries could be used effectively in the DHTs that use order preserving hash functions. DHTs that use universal hashing like Chord might not be a very good place to employ range queries. Order preserving hash functions are needed to maintain the semantic proximity of the keys. If the semantically closer keys are stored close to each other then that would ensure that the query can be completed in the minimum number of hops. The overlay network of the DHT should use a data-structure that facilitates semantic proximity. Trie is such a data-structure.
Trie is an ordered tree data structure that is used to store an associative array where the keys are strings. The position of the node in the tree shows what key it is associated with it.
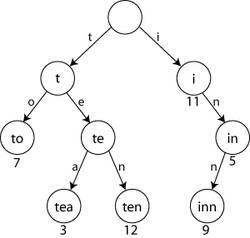 |
| Figure 8: A trie for keys "to", "tea", "ten", "i", "in", and "inn". Image courtesy Wikipedia |
Now we know that range queries are more suitable for DHTs that preserve semantic proximity and uses suitable data-structure like trie as the overlay network. P-Grid is such a DHT that uses trie as the overlay network. Each peer in P-Grid is a leaf in the trie binary tree, leaf corresponding to a binary string. Each peer stores a set of data items, whose keys are calculated using an order preserving hash function such that the path of the peer is the prefix of the key of each data item it stores. The routing table of a peer contains the address of at least one peer from each subtree of the trie binary tree so that it can send a query to any peer in the tree. Each Peer might also have a few replica nodes for data security.
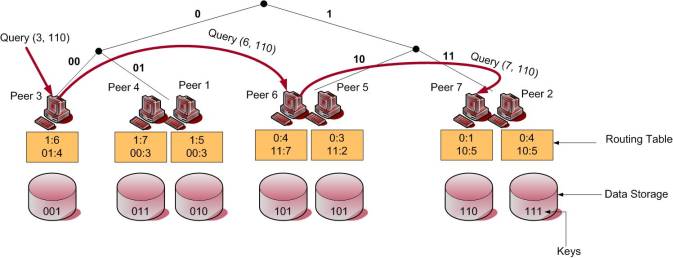 |
| Figure 9: P-Grid overlay network and routing scheme (Click on image to expand) |
Figure (9) presents an example of the topology of P-Grid. The overlay network is a trie binary tree and the peers are at the leaves. Looking at the data keys stored by the peers we see that the keys are prefixed with the path of the peer, this being a result of using order preserving hash functions. The routing table of the peers contain the path to the peers from other subtrees such that this peer has the ability to route a query to any other peer in any part of the network. Figure (9) also shows an example of a query routing. The query is looking for data key '110' and is forwarded to peer 3 by the requester. Looking at the key, peer 3 knows that the key is with some peer in the subtree where paths start with '1'. Peer 3 know the address of peer 6 that happens to be in that part of the network and so the query is forwarded to peer 6. Peer 6, after looking at the query knows that it should go to a peer in the subtree where paths start with '11' and so it forwards the query to peer 7. Peer 7 happens to have the key the query is attempting to find so the search ends here.
Karl Aberer, et. al. propose in [5] that a range query can be executed on an order preserving DHT in one of two ways -
In Min-max traversal algorithm, range queries are processed sequentially by starting from a peer holding data items belonging to one bound of the range and forwarding the query to a peer responsible for the next partition of the key space, until a peer responsible for the other bound of the range is encountered.
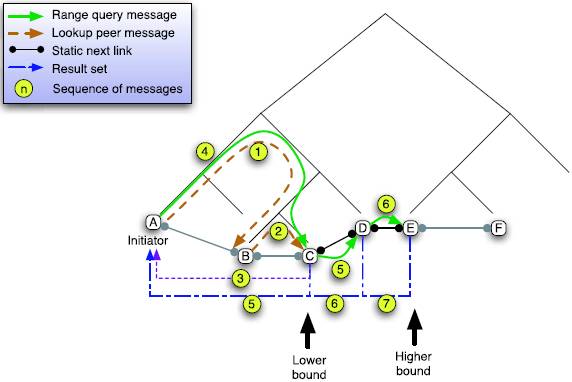 |
| Figure 10: Min-max traversal method. Image source [ 5 ] |
The example in figure (10) shows a range query initiated by the peer A. Peer C is the lower bound of this query and peer E forms the upper bound. The lower bound is found using typical P-Grid routing mechanism (A -> B -> C). At this point A sends the range query to C. C returns the dataset to A and checks if it is the upper bound of the query, which it is not. C then forwards the query to peer D and the same process that took place at C is repeated here also. This keeps on happening till the query reaches its upper bound, i.e. peer E. Here E finds that it is the upper bound of the query and hence it just returns the dataset to A and doesn't forward the query to any node.
Shower algorithm processes range queries by doing them concurrently and recursively. The range query is first forwarded to an arbitrary peer responsible for any of the key space partitions within the range, and then the query is forwarded to the other partitions in the interval using this peer's routing table.
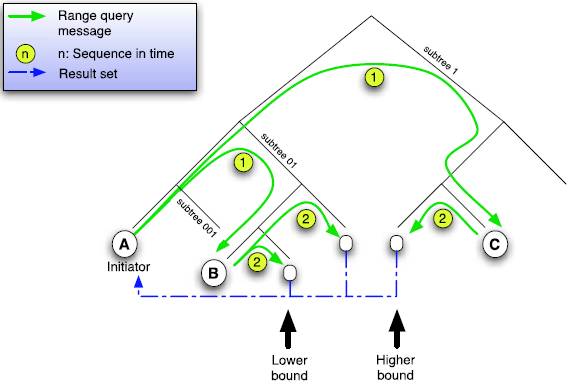 |
| Figure 11: Shower method. Image source [ 5 ] |
In this case the query might be sent to many peers that are outside the bounds of the range. When a peer gets the query it checks its routing table for any peer that could be in the range of the query and if it finds any then it forwards the query to that peer. The peer also checks if it itself is in the range or not. And if it is then it returns the dataset to the requester. So there could be many redundant messages but this might be the faster of the two methods because many peers work on the query at the same time.
A Hierarchical DHT like Cyclone, proposed by Marc Sánchez Artigas in [4] brings the benefits of locality awareness and multi-pathing together. Since Cyclone is a horizontal HDHT, all the leaf overlay networks are connected using single DHT. This forms the basis of conceptual hierarchy and routing efficiency. DHTs following different protocols can co-exist in Cyclone.
An effective routing scheme is essential to accomplish search efficiency. For routing efficiency, Cyclone assigns a unique 'b' bit identifier to each node. This ID consists of two parts -
Thus the combination of prefix and suffix make up a unique ID for the peer in the whole network. It is important to make the cluster ID a part of the node identifier, as this would enable efficient routing.
To make sure that a query can reach its destination cluster in maximum 'L' number of hops, where 'L' is the length of the cluster ID of the bottom-most cluster in the tree, Cyclone applies the XOR metric link creation rule. This means that every peer 'm' has to have at least p = |Suffix(m)| inter cluster links.
When a peer 'n' wants to lookup for a key, say 'k', the first step is to look within the own cluster to take advantage of the network locality. If the peer hosting 'k' is found then the search stops at this step. However if 'k' is not found then the query reaches the closest predecessor 'p' of 'k'. To find the cluster for 'k', the search algorithm takes |Suffix(p)| rightmost bits of 'k' and uses it to find the XOR distance to every cluster in the routing table of 'p'. This way a candidate cluster is found and the query is forwarded to an arbitrary peer in the candidate cluster. If the candidate cluster is not the destination cluster then the process that took place at 'p' is repeated till the query reaches the destination cluster. After the query reaches the destination cluster, the manager peer 'm' for the key 'k' is found and the query is passed to it. This whole process is illustrated in figure (12) below.
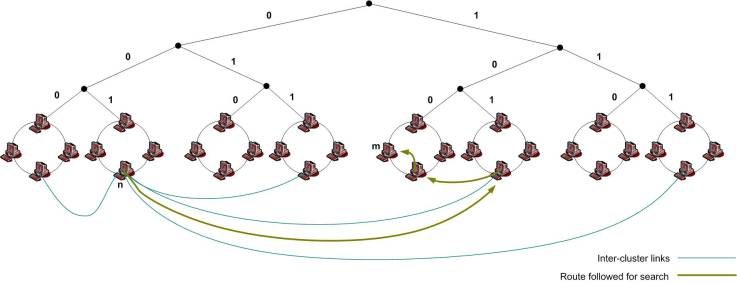 |
| Figure 12: The Cyclone topology and an example of query routing from peer n to m (Click on image to expand) |
|
Conventional Flooding |
Random Walk |
Percolation Search |
HDHT |
Range Query |
|
Performed on unstructured P2P networks |
Performed on unstructured P2P networks |
Performed on unstructured P2P networks |
Performed on DHT P2P networks |
Performed on DHT P2P networks |
|
Works same with any network |
Works best with multiple queries and peer clustering |
Works best with Power Law networks |
Works same with all the DHTs |
Works best when semantic proximity of keys is maintained |
|
On average search is done in k * N time (k = avg degree of nodes, N = total number of nodes) |
On average search is done in log time |
On average search is done in log time |
On average search is done in log time |
On average search is done in log time |
|
Returns single result |
Returns single result |
Returns single result |
Returns single result |
Returns a set of results |
|
Very wasteful of resources, as every peer processes each query |
Less taxing on resources |
Much taxing on resources as it requires lot of pre-search preparation steps and extra storage |
Not too taxing on resources |
Min-max algorithm uses resources wisely |
|
Is not very fast, as every peer processes each query |
Result are reasonably fast |
Search should be very fast, as many peers process the query simultaneously |
Routing is very fast |
Shower algorithm is very fast |
|
Works same for all cases |
Not suitable for all cases |
Not suitable for all cases |
Works same for all cases |
Not suitable for all cases |
We surveyed some of the advanced search techniques for P2P networks in this paper. The techniques discussed here are suitable in certain type of networks and work best when certain conditions are met. Outside these conditions these technique might not provide any improvement in search process. So these search techniques should not be only means of search. They should be used along with other more general purpose search techniques for the best results. In summary, the ideal usage should be -
HDHTs are a useful architecture when the search would be done in a big network with a large number of peers and where scalability is an issue.
[1] Nima Sarshar, P. Oscar Boykin, Vwani P. Roychowdhury, "Percolation Search in Power Law Networks: Making Unstructured Peer-To-Peer Networks Scalable", in proceedings of IEEE International Conference on Peer-to-Peer Computing, 2004
[2] Christos Gkantsidis, Milena Mihail, Amin Saberi, "Random Walks in Peer-to-Peer Networks", in proceedings of IEEE Infocom, 2004
[3] Abhishek Gupta, Divyakant Agrawal, Amr El Abbadi, "Approximate Range Selection Queries in Peer-to-Peer Systems", in proceedings of Conference on Innovative Data Systems Research (CIDR), 2003
[4] Marc Sánchez Artigas, Pedro García López, Jordi Pujol Ahulló, Antonio F. Gómez Skarmeta, "Cyclone: a Novel Design Schema for Hierarchical DHTs", in proceedings of IEEE International Conference on Peer-to-Peer Computing, 2005
[5] Anwitaman Datta, Manfred Hauswirth, Renault John, Roman Schmidt, Karl Aberer, "Range queries in trie-structured overlays", in proceedings of IEEE International Conference on Peer-to-Peer Computing, 2005
[6] Artur Andrzejak, Zhichen Xu, "Scalable, Efficient Range Queries for Grid Information Services", in proceedings of IEEE International Conference on Peer-to-Peer Computing, 2002
[7] Qin Lv, Kai Li, Pei Cao, Edith Cohen, Scott Shenker, "Search and Replication in Unstructured Peer-to-Peer Networks", in proceedings of 16th International Conference on Supercomputing
Search was conducted on different IEEE digital libraries like the IEEE Computer Society and IEEE Communication Society. Search was also conducted on the ACM and CIDR digital libraries. Papers related to the keywords were the primary reference for this survey. Other papers listed in the reference section were reviewed because of their presentation of the important technical issues related to the keywords.